Hong's External Brain

Appearance

在上一小节中，我们已经成功的构建了逻辑回归的损失函数，但由于逻辑回归模型是分类模型，因此我们在构建损失函数时，采用了极大似然估计或者交叉熵的方法，并且由于损失函数也是分类模型的损失函数，所以求解损失函数的参数也无法使用最小二乘法，而是使用本节要学的梯度下降法。

当然，这其实也不仅仅是逻辑回归模型的“问题”，对于大多数机器学习模型来说，损失函数都无法直接利用最小二乘法进行求解。此时，就需要我们掌握一些可以针对更为一般函数形式进行最小值求解的优化方法。而在机器学习领域，最为基础、同时也最为通用的方法就是梯度下降算法。

本节我们将详细讨论梯度下降算法的基本原理和实现方法，并在此基础上尝试对逻辑回归损失函数进行求解。

梯度下降基本原理与学习率（Learning Rate） ​

梯度的基本概念 ​

我们需要回顾Lesson 2中所介绍的关于梯度向量的相关概念。Lesson 2中我们曾提及，设$f(x)$是一个关于$x$的函数，其中$x$是向量变元（就是向量套向量），并且$$x = [x_1, x_2,...,x_n]^T$$

则： $$ \frac{\partial f}{\partial x} = [\frac{\partial f}{\partial x_1}, \frac{\partial f}{\partial x_2}, ..., \frac{\partial f}{\partial x_n}]^T $$ 而该表达式也被称为向量求导的梯度向量形式。 $$ \nabla _xf(x) = \frac{\partial f}{\partial x} = [\frac{\partial f}{\partial x_1}, \frac{\partial f}{\partial x_2}, ..., \frac{\partial f}{\partial x_n}]^T $$ 进一步的，如果假设$f(x)$是关于参数$x$的损失函数，则$\nabla _xf(x)$就是损失函数的梯度向量，或者梯度表达式。而当损失函数的参数$x$选定一组取值之后，我们就能计算梯度表达式的取值，该值也被称为损失函数在某组参数取值下的梯度。

在梯度下降算法中，参数的移动方向是梯度的负方向。

梯度下降的过程 ​

例如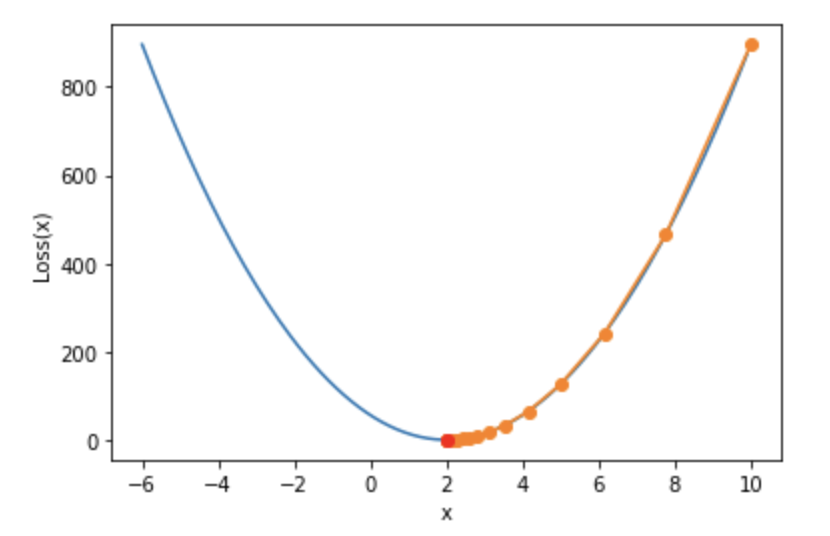：image-20241006145014884

举个🌰，说明梯度下降的一次迭代 ​

我们将先从一个简单的例子入手，来查看梯度下降的一般过程，然后我们再进行更加严谨的理论推导。

例如，有简单数据集表示如下：

xy
12
24
36

其中$x$是数据集特征，$y$是数据集标签，假设，我们使用简单线性回归$y = wx$对该组数据进行拟合，则此处我们可以构造损失函数如下： $$ \begin{align} SSELoss(w) & = (2-1w)^2 + (4-2w)^2 + (6-3*w)^2 \ & = w^2-4w+4+4w^2-16w+16+9w^2-36w+36 \ & = 14w^2-56w+56 \ & = 14(w^2-4w+4) \ & = 14(w-2)^2 \end{align} $$ 然后对这个损失函数使用梯度下降法求解参数$w$

Step 1.随机选取初始参数值 ​

在上述例子中，参数只有一个，我们可以随机设置一个初始的参数值，例如我们令$w_0=10$。

Step 2.基于$w_0$，确定参数移动方向 ​

由于损失函数$f(w)$： $$ f(w) = 14(w-2)^2 $$ 因此损失函数的梯度向量表示形式为： $$ \nabla _wf(w) = \frac{\partial f}{\partial w}=28(w-2) $$ 代入Step1中随机选取的初始值$w_0=10$，则梯度计算结果为 $$ \nabla _wf(w_0)=28(10-2)=28*8=224 $$

上述计算结果中，224既是梯度的取值，同时也代表着梯度的方向——正方向。

而在梯度下降法中，参数移动的方向应该是梯度的负方向，因此此时参数减少的方向应该是负方向，和上述损失函数图像观测结果相同。

注意，如果损失函数包含多个参数的话，参数组变化方向就有多个，例如假设参数组包含两个参数$w=(a,b)$，则$w$的变化就相当于是在$(a, b)$这个二维平面上的点发生移动。

Step 3.确定移动步长（学习率，Learning Rate）并进行移动 ​

在确定移动的方向之后，接下来需要进一步确定移动距离。在梯度下降中，我们采用梯度乘以某个人工设置的参数作为每一步移动的距离，这个参数被称为步长或者学习率（Learning rate）。

例如在这个例子中，我们设置学习率为$lr = 0.01$，则从$w_0$进行移动的距离是$0.01 * 224 = 2.24$，而又是朝向梯度的负方向进行移动，因此$w_0$最终移动到了$w_1 = 10-2.24 = 7.76$

相比于步长，将人工设置的参数称为学习率会更加贴切，该参数并不代表真实移动的距离，而是影响真实移动距离的一个“比率”，或者说是真实移动距离学习梯度值的“比率”。

至此，参数$w$就完成了第一次移动，$w_0 \rightarrow w_1$。

梯度下降的多轮迭代 ​

当然，$w$从$w_0$移动到$w_1$其实只移动了一步，要最终抵达损失函数的最小值点$w=2$，还有很长一段距离，因此我们还需要移动多次。

参数多次移动过程中的每一步其实都是在重复上述三个步骤。例如，当我们需要第二次移动$w$时，过程如下： $$ w_2 = w_1 - lr \cdot \nabla _wf(w_1) $$ 即$w_2$等于$w_1$沿着$w_1$的负梯度方向移动了$lr\cdot\nabla _wf(w_1)$距离之后得到的结果。此时我们是在$w_1$的基础上，减去学习率和$w_1$梯度的乘积。

当然，依此类推，当从$w_{(n-1)}$移动到$w_n$时$w_n$的计算公式如下： $$ w_n = w_{(n-1)} - lr \cdot \nabla wf(w) $$ 并且，我们可以称从$w_0$移动到$w_1$是第一轮迭代，从$w_1$移动到$w_2$是第二轮迭代，从$w_{(n-1)}$移动到$w_n$是第n轮迭代。

迭代其实是一个数学意义上的概念，一般指以下计算流程：某次运算时初始条件是上一次运算的结果，而当前运算的结果则是下一次计算的初始条件。

而通过带入梯度值进行多轮迭代，最终使得损失函数的取值逐渐下降的算法，就被称为梯度下降。

梯度下降算法特性与学习率 ​

首先，我们简单验证，经过上述梯度下降的一系列计算，最终能否有效降低损失函数的计算结果，即使得𝑤最终朝向最优值2靠拢。

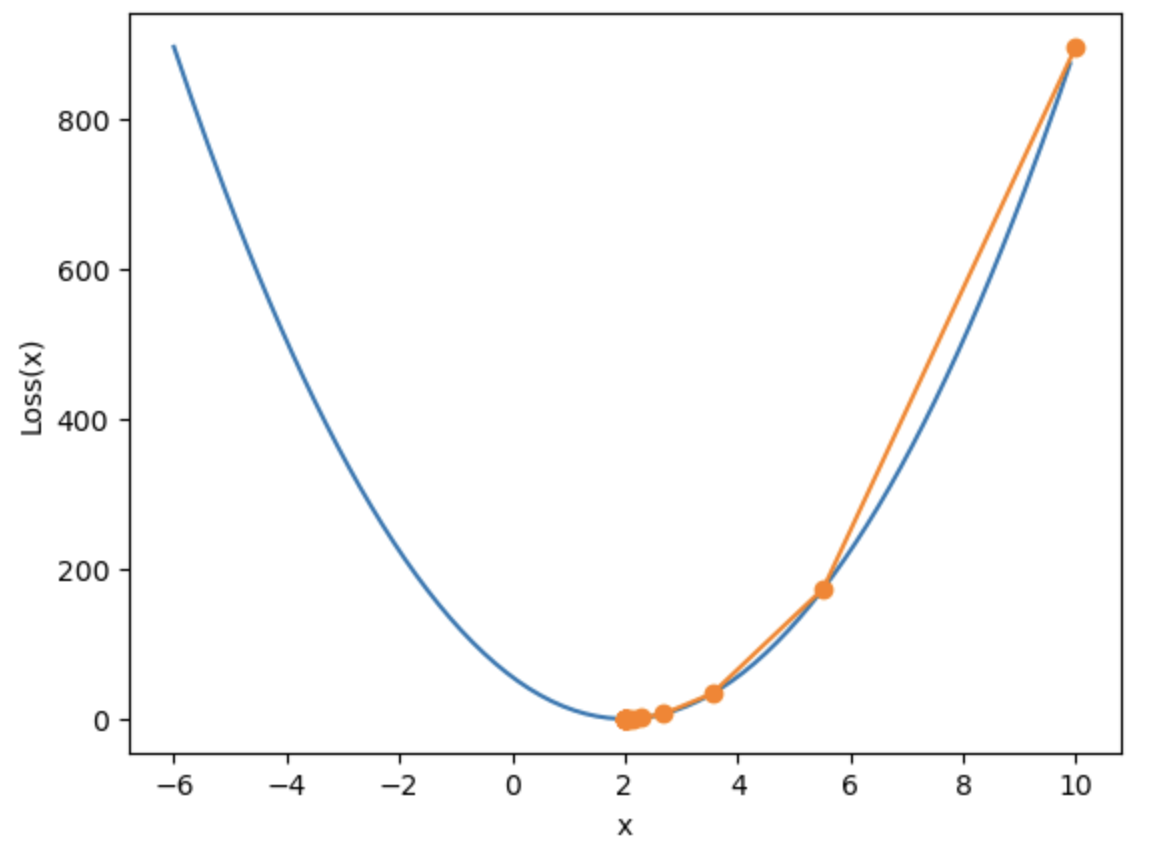
image-20241006163602143

上图，蓝色的线为损失函数的真实取值画图，橘色的为梯度下降法计算的损失函数值的变化过程。可以看出，梯度下降法可以有效的降低损失值。

接下来，根据上图我们详细讨论：

  • 梯度下降算法的基本特性
  • 超参数取值一般规范。（学习率的设置范围）

梯度下降算法的基本特性 ​

从图像上，我们发现，梯度下降的计算过程中，刚开始$w$变化非常快，而随着逐渐接近最小值点$w$的变化幅度逐渐减少，也就是说，梯度下降其实并不是一个等步长的移动过程。当然，根据梯度下降的计算公式，$w_{(n-1)}$和$w_{n}$的差值是： $$ |w_n - w_{(n-1)}| = |lr \cdot \nabla wf(w)| $$ 而lr又是一个恒定的数值，那么也就是说，每个点的梯度值是不一样的（哪怕梯度方向一样），并且越靠近最小值点梯度值越小，当然这点从梯度计算公式也能看出： $$ \nabla _wf(w) = \frac{\partial f}{\partial w}=28(w-2) $$ 当然，这也就等价说明，如果某点的梯度值相对较大，那么该点应该距离全域最小值较远。

学习率的设置范围 ​

在学习率对移动距离进行修正时，学习率不宜设置过小，也不宜设置过大，

当学习率设置得过小时： ​

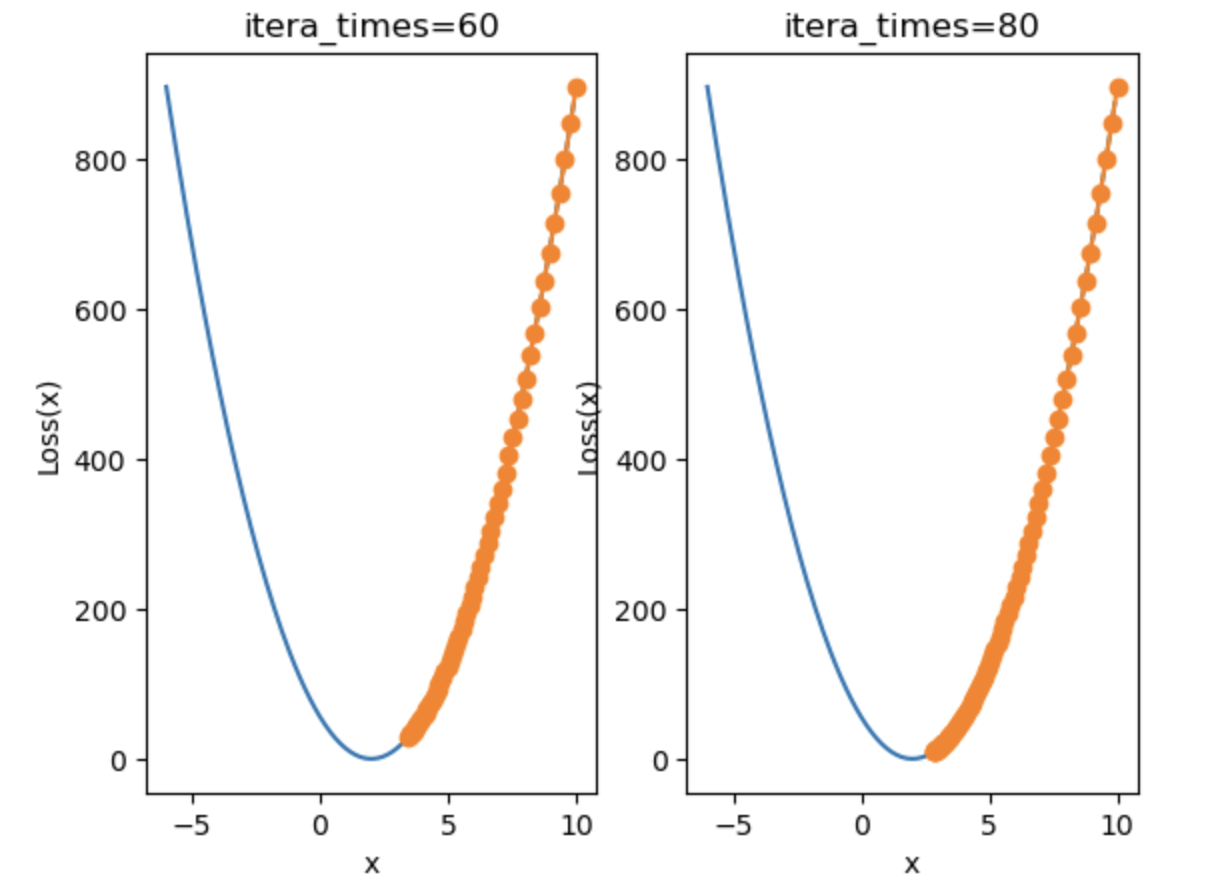
image-20241006165706901

当学习率设置得过大时： ​

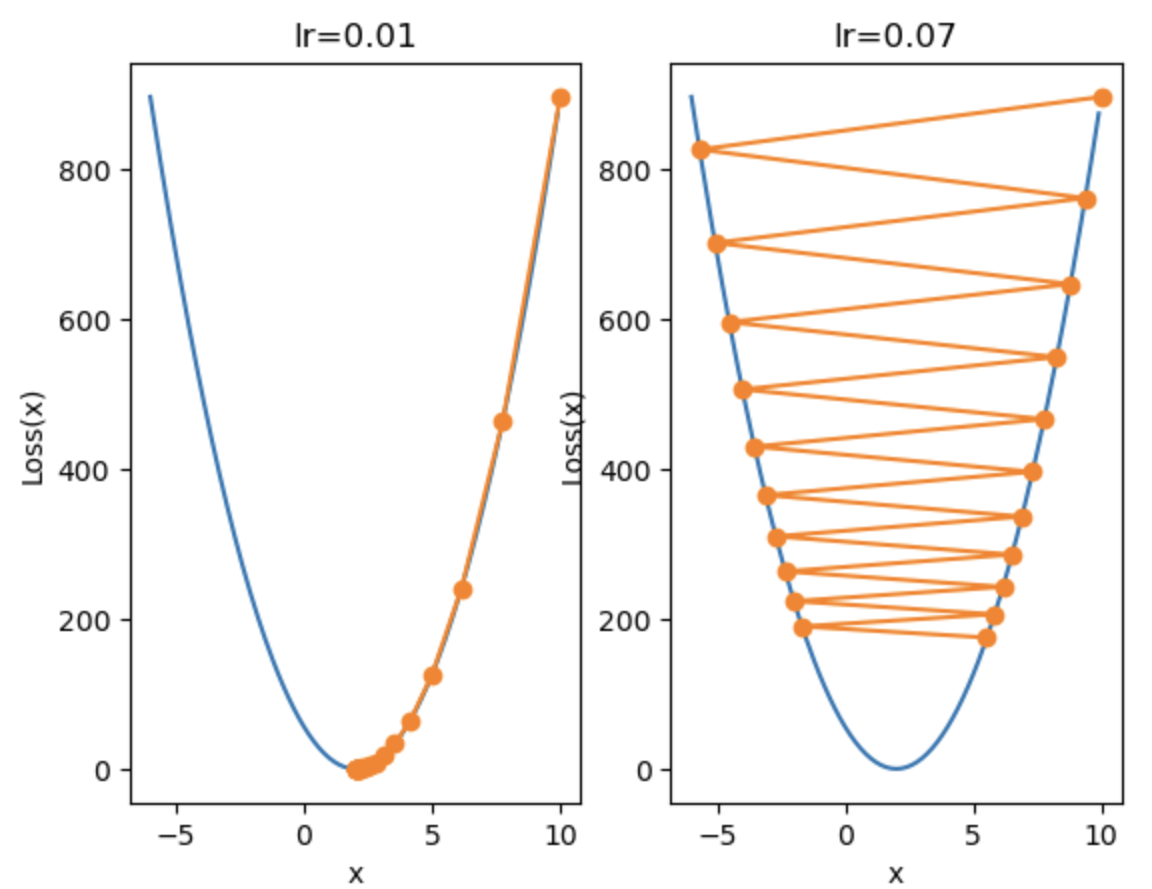
image-20241006165823818

损失值将到200左右就不再降了，无法收敛

当$lr= 0.08$时：

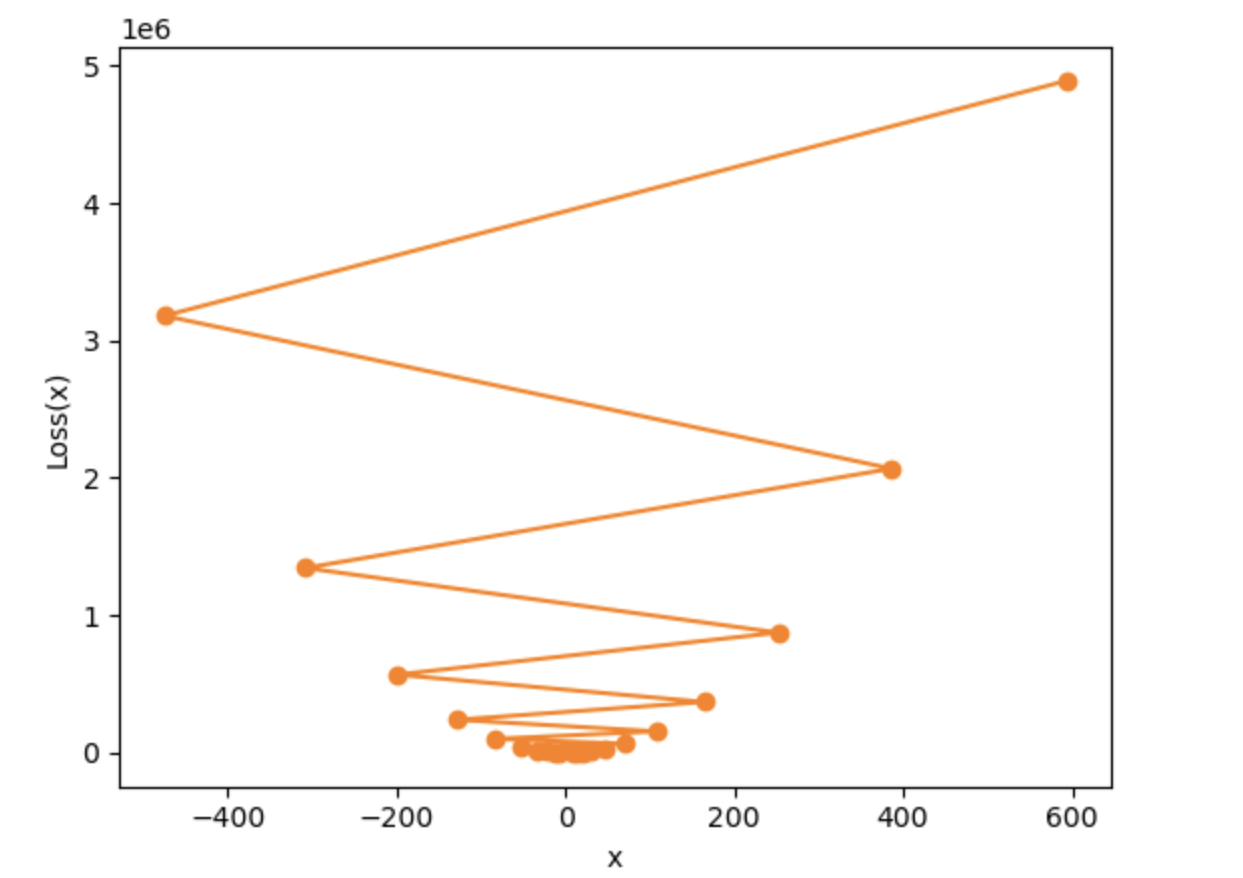
image-20241006165936596

损失值越来越大，参数没有收敛，反而发散了

因此，当设置了过大的学习率时：

梯度下降一般建模流程与多维度梯度下降 ​

1.多维梯度下降与损失函数可视化 ​

一种更为一般的情况是，一个模型中包含多个参数，而损失函数就是这多个参数共同构成的函数。

例如在Lesson 1中我们曾利用带截距项的简单线性回归𝑦=𝑤𝑥+𝑏y=wx+b对下述数据进行拟合，并得出带有两个参数的损失函数：

数据特征参数组模型输出数据标签
Whole weight(x)$(w,b)$$\hat y$Rings(y)
1(w, b)w+b2
3(w, b)3w+b4

$$ SSELoss(w, b) = (y_1 - ŷ_1)^2 + (y_2 - ŷ_2)^2 = (2 - w - b)^2 + (4 - 3w - b)^2 $$

而此时损失函数图像就是包含两个变量的三维图像

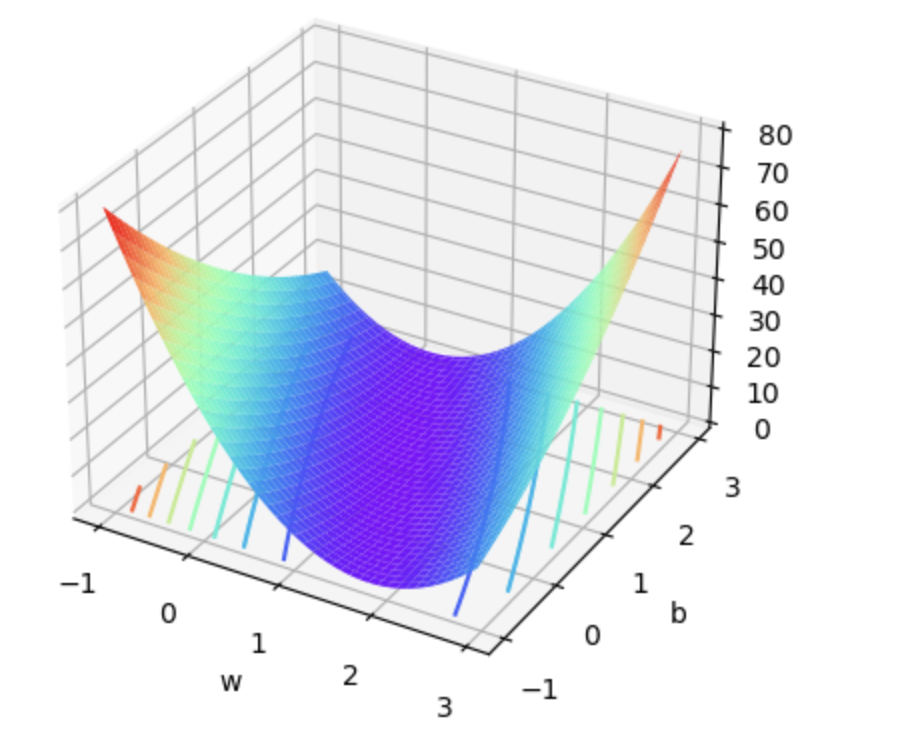
image-20241012121125238

并且，我们通过最小二乘法能够找出全域最小值点为(1,1)，也就是当𝑤=1,𝑏=1w=1,b=1时，能够让损失函数取值最小。当然，围绕该问题，我们也可以采用梯度下降进行最优解求解。

画图代码在代码.ipynb里，自己去看。

2.梯度下降计算流程 ​

  • Step 1.确定数据及模型

    • 首先还是要明确数据和模型，然后才能进一步确定参数、梯度计算公式等变量。
    • 例如：以$y=wx+b$简单线性回归对上述简单数据集进行拟合，参数向量包含两个分量。

  • Step 2.设置初始参数值

    • 一般做法是，给初始参数赋予一组随机数作为初始取值

  • Step 3.根据损失函数求出梯度表达式

    • 只有确定了梯度表达式，才能在后续每一轮迭代过程中快速计算梯度。

    • 以线性回归举例的话，线性回归的损失函数是围绕SSE及其衍生的指标所构建的损失函数，此处以MSE作为损失函数的构建指标，此处可借助已经定义好的SSELoss函数执行计算。

    • $$ MSELoss(\hat w) = \frac{||y - X\hat w||_2^2}{m} = \frac{(y - X\hat w)^T(y - X\hat w)}{m} $$

    • 而对于线性回归损失函数梯度表达式，则可对损失函数梯度求导结果得出： $$ \begin{aligned} \frac{SSELoss(\hat w)}{\partial{\boldsymbol{\hat w}}} &= \frac{\partial{||\boldsymbol{y} - \boldsymbol{X\hat w}||_2}^2}{\partial{\boldsymbol{\hat w}}} \ &= \frac{\partial(\boldsymbol{y} - \boldsymbol{X\hat w})^T(\boldsymbol{y} - \boldsymbol{X\hat w})}{\partial{\boldsymbol{\hat w}}} \ & =\frac{\partial(\boldsymbol{y}^T - \boldsymbol{\hat w^T X^T})(\boldsymbol{y} - \boldsymbol{X\hat w})}{\partial{\boldsymbol{\hat w}}}\ &=\frac{\partial(\boldsymbol{y}^T\boldsymbol{y} - \boldsymbol{\hat w^T X^Ty}-\boldsymbol{y}^T\boldsymbol{X \hat w} +\boldsymbol{\hat w^TX^T}\boldsymbol{X\hat w})}{\partial{\boldsymbol{\hat w}}}\ & = 0 - \boldsymbol{X^Ty} - \boldsymbol{X^Ty}+X^TX\hat w+(X^TX)^T\hat w \ &= 0 - \boldsymbol{X^Ty} - \boldsymbol{X^Ty} + 2\boldsymbol{X^TX\hat w}\ &= 2(\boldsymbol{X^TX\hat w} - \boldsymbol{X^Ty}) \ &= 2X^T(X\hat w -y) \end{aligned} \ $$ 此处我们使用MSE作为损失函数，则该损失函数的梯度表达式为： $$ \frac{MSELoss(\hat w)}{\partial{\boldsymbol{\hat w}}} = \frac{2X^T(X\hat w -y)}{m} $$

  • Step 4.执行梯度下降迭代

    • 在给定梯度计算公式和参数初始值的情况下，我们就能够开始进行梯度下降迭代计算了。在梯度下降过程中，参数更新参照如下公式：

    • $$ w_n = w_{(n-1)} - lr \cdot \nabla wf(w) $$

3.二维梯度下降过程的可视化展示 ​

等高线图 ​

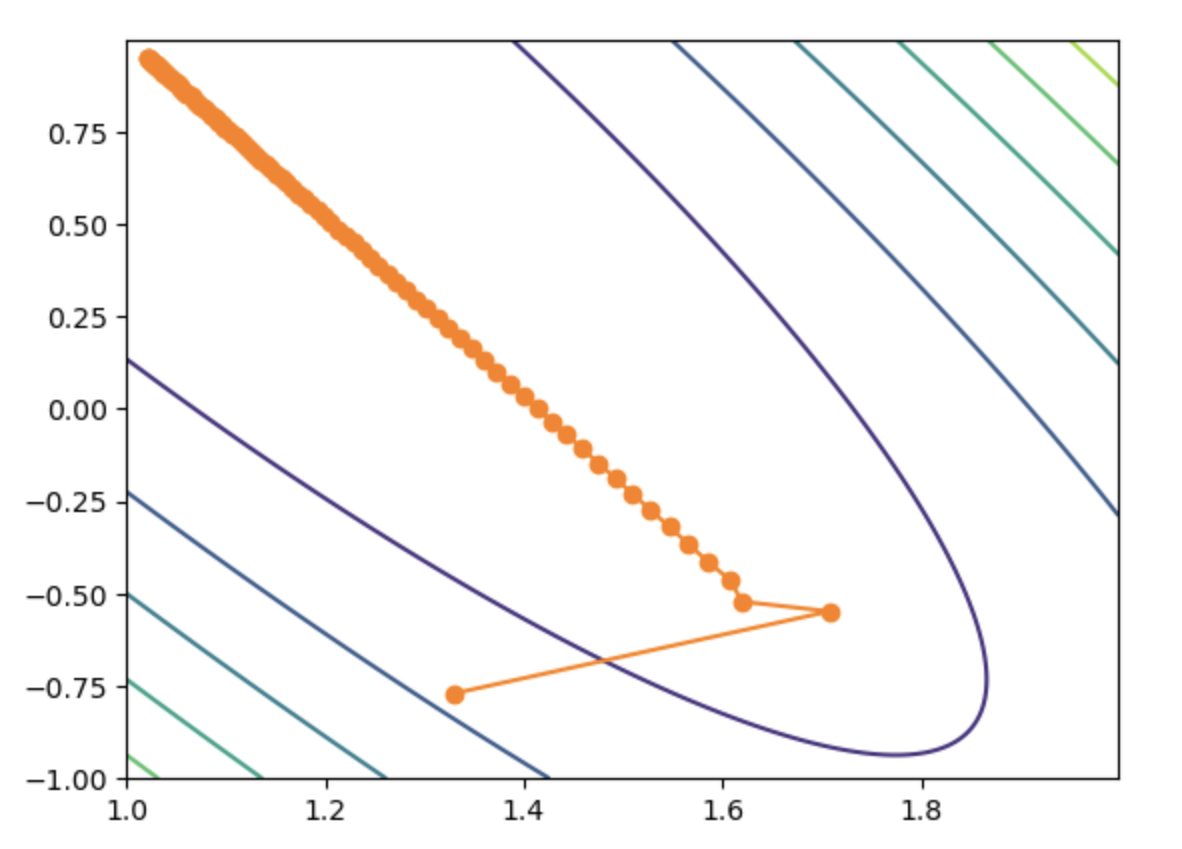
image-20241012124135390

假设现在模型有两个参数，比如$y=w_1\cdot x_1 + w_2 \cdot x_2$，那么在上图的等高线图中，横轴为参数1:$w_1$，纵轴为参数2:$w_2$，每一条等高线表示一个常数的损失函数值，等高线上的所有点具有相同的损失函数值。等高线越靠近内圈，损失函数的值越小

从上图可以看出，随着梯度下降，参数值的迭代更新，损失函数值越来越小。

画图代码在代码.ipynb里，自己去看。

损失函数取值变化图 ​

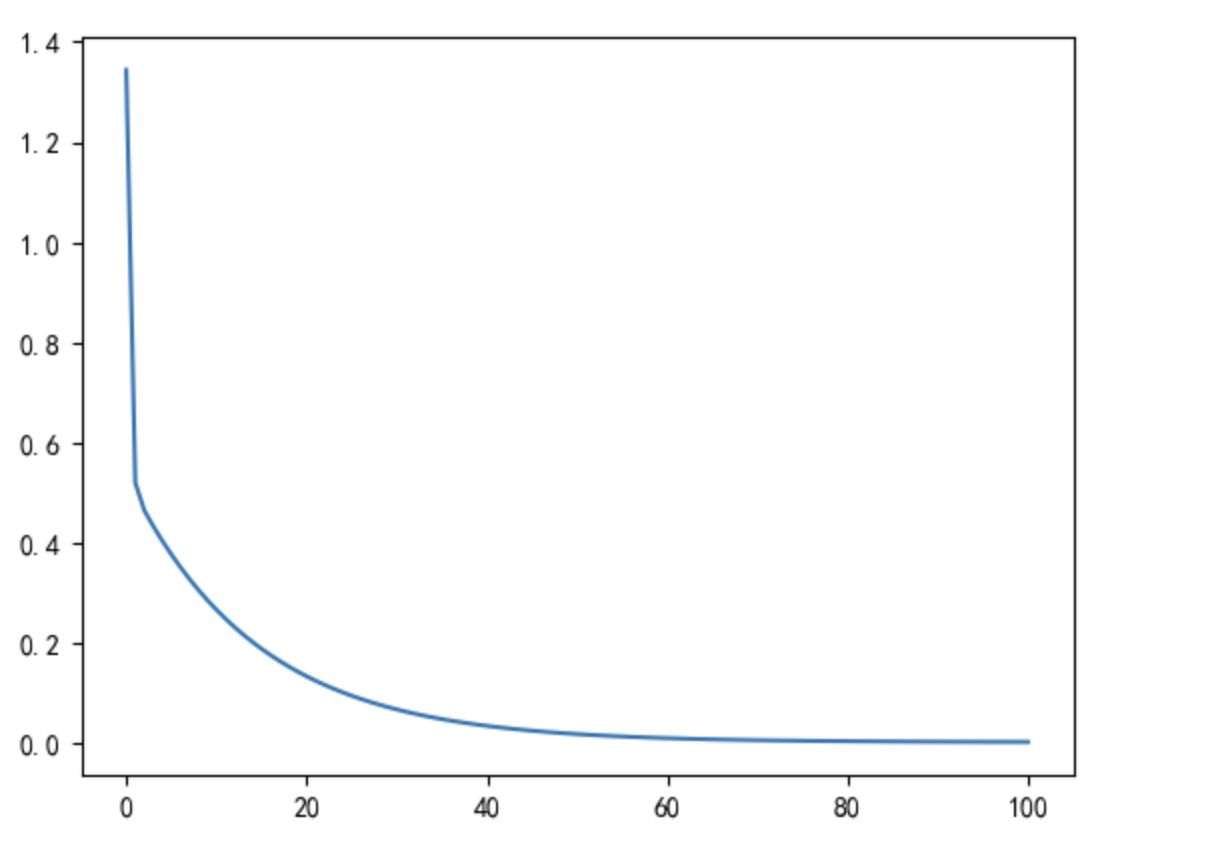
image-20241012125203423

横轴为迭代次数，纵轴为损失函数值。

同样的可以看出，随着梯度下降进行，参数值迭代更新，损失函数的值越来越小。