根据逻辑回归的基本公式: $$ y = \frac{1}{1+e^{-(\hat w^T \cdot \hat x)}} $$ 不难看出,逻辑回归的参数其实就是线性方程中的自变量系数和截距。不过由于加入了联系函数,逻辑回归的参数并不能像线性回归一样利用最小二乘法进行快速求解。
当然,和所有的机器学习模型一样,要求解模型参数,就先必须构造损失函数,然后根据损失函数的基本情况寻找优化算法求解。对于逻辑回归来说,此处介绍两种不同的方法来创建和求解损失函数,两种方法出发点各不相同但却殊途同归:
- 极大似然估计(Maximum Likelihood Estimate)
- 通过相对熵(relative entropy)构建交叉熵损失函数
逻辑回归参数估计基本思路
因此先通过一个简单的例子来讨论关于逻辑回归的参数估计的基本思路,即损失函数构建和求解的一般思路。
1.构建损失函数
现有简单数据集如下:
| sepal_length | species |
|---|---|
| 1 | 0 |
| 3 | 1 |
由于只有一个特征,因此可以构建逻辑回归模型为: $$ y=sigmoid(wx+b)=\frac{1}{1+e^{-(wx+b)}} $$ 我们将模型输出结果视作y=1概率,则分别带入两条数据可得模型输出结果为: $$ p(y=1|x=1)=\frac{1}{1+e^{-(w+b)}} \ p(y=1|x=3)=\frac{1}{1+e^{-(3w+b)}} $$ 其中$p(y=1|x=1)$表示$x$取值为1时$y$取值为1的条件概率。而我们知道,两条数据的真实情况为第一条数据$y$取值为0,而第二条数据$y$取值为1,因此我们可以计算$p(y=0|x=1)$如下: $$ p(y=0|x=1) = 1-p(y=1|x=1)=1-\frac{1}{1+e^{-(w+b)}}=\frac{e^{-(w+b)}}{1+e^{-(w+b)}} $$ 即:
| sepal_length | species | 0-predict | 1-predict |
|---|---|---|---|
| 1 | 0 | $\frac{1}{1+e^{-(w+b)}}$ | |
| 3 | 1 | $\frac{e^{-(3w+b)}}{1+e^{-(3w+b)}}$ |
此处如果我们希望模型预测结果尽可能准确,就等价于希望𝑝(𝑦=0|𝑥=1)p(y=0|x=1)和𝑝(𝑦=1|𝑥=1)p(y=1|x=1)两个概率结果越大越好。因此可以获得下式: $$ p(y=0|x=1)\cdot p(y=1|x=3) $$ 即我们希望x=1,y=0和x=3,y=1同时发生的概率越大越好。
此外,考虑到损失函数一般都是求最小值,因此可将上式求最大值转化为对应负数结果求最小值,同时累乘也可以转化为对数相加结果,因此上式求最大值可等价于下式求最小值: $$ \begin{aligned} LogitLoss(w, b)&=-ln(p(y=1|x=3))-ln(p(y=0|x=1)) \ &=-ln(\frac{1}{1+e^{-(3w+b)}})- ln(\frac{e^{-(w+b)}}{1+e^{-(w+b)}}) \ &=ln(1+e^{-(3w+b)})+ln(1+\frac{1}{e^{-(w+b)}}) \ &=ln(1+e^{-(3w+b)}+e^{(w+b)}+e^{-2w}) \end{aligned} $$
回顾此前内容:损失函数和带入数据量息息相关。
为什么逻辑回归的损失函数不能采用和之前一样的SSE的思路构建?
在将模型高准确率的诉求具象化为$p(y=0|x=1)\cdot p(y=1|x=3)$参数的过程,此处我们为何不能采用类似SSE的计算思路取构建损失函数,即进行如下运算: $$ ||y-yhat||_2^2=||y-\frac{1}{1+e^{-(\hat w^T \cdot \hat x)}}||_2^2
$$ 其根本原因在于,。而相比之下,概率连乘所构建的损失函数是凸函数,可以快速求解出全域最小值。
概率连乘所构建的损失函数为: $$ \text{LogitLoss}(w, b) = \ln(1 + e^{-(3w + b)}) + \ln(1 + e^{-(w + b)}) $$ 该损失函数一阶导为: $$ \frac{\partial \text{LogitLoss}(w, b)}{\partial w} = \frac{-3e^{-(3w + b)}}{1 + e^{-(3w + b)}} + \frac{-e^{-(w + b)}}{1 + e^{-(w + b)}} $$ 该损失函数二阶导为: $$ \frac{\partial^2 \text{LogitLoss}(w, b)}{\partial b^2} = \frac{e^{-(3w + b)}}{(1 + e^{-(3w + b)})^2} + \frac{e^{-(w + b)}}{(1 + e^{-(w + b)})^2} $$ 很明显,二阶导> 0,概率连乘所构建的损失函数为凸函数。
还有一个原因是概率连乘的模型可以转换为,对数相加,减少计算量,节约计算资源。
2.损失函数求解
从数学角度可以证明,按照上述构成构建的逻辑回归损失函数仍然是凸函数,此时我们仍然可以通过对LogitLoss(w,b)求偏导然后令偏导函数等于0、再联立方程组的方式来对参数进行求解。 $$ \frac{\partial LogitLoss(w,b)}{\partial w}=0 \ \frac{\partial LogitLoss(w,b)}{\partial b}=0 $$ 值得一提的是,上述构建损失函数和求解损失函数的过程,也被称为极大似然估计。接下来我们就将极大似然估计的方法推广到一般过程。
极大似然估计损失函数(参数估计)
接下来,我们考虑更为一般的情况,围绕逻辑回归方程的一般形式,采用极大似然估计方法进行参数估计:
逻辑回归模型: $$ y = \frac{1}{1+e^{-(\hat w^T \cdot \hat x)}} $$ 其中: $$ \hat w = [w_1,w_2,...w_d, b]^T, \hat x = [x_1,x_2,...x_d, 1]^T $$ 求解过程总共分为四个步骤,分别是:
Step1:确定似然项
所谓似然函数,可简单理解为前例中累乘的函数。而累乘过程中的每个项,可称为似然项,因此,似然项其实和数据是一一对应的,带入多少条数据进行建模,似然函数中就有多少个似然项。
对于逻辑回归来说,当$\hat w$和$\hat x$取得一组之后,既可以有一个概率预测输出结果,即: $$ p(y=1|\hat x;\hat w) = \frac{1}{1+e^{-(\hat w^T \cdot \hat x)}} $$ 而对应$y$取0的概率为: $$ 1-p(y=1|\hat x;\hat w) =1- \frac{1}{1+e^{-(\hat w^T \cdot \hat x)}}=\frac{e^{-(\hat w^T \cdot \hat x)}}{1+e^{-(\hat w^T \cdot \hat x)}} $$ 我们可以令 $$ p_1(\hat x;\hat w)=p(y=1|\hat x;\hat w) \ p_0(\hat x;\hat w)=1-p(y=1|\hat x;\hat w) $$
$$ p_1(\hat x;\hat w)^{y_i} \cdot p_0(\hat x;\hat w)^{(1-y_i)} $$ 其中,$y_i$表示第$i$条数据对应的类别标签。不难发现,当$y_i=0$时,代表的是$i$第条数据标签为0,此时需要带入似然函数的似然项是$p_0(\hat x;\hat w)$(因为希望$p_0$的概率更大)。反之,当$y_i=1$时,代表的是$i$第条数据标签为1,此时需要带入似然函数的似然项是$p_1(\hat x;\hat w)$。上述似然项可以同时满足这两种不同的情况。
Step 2.构建似然函数
接下来,通过似然项的累乘计算极大似然函数: $$ \prod^N_{i=1}[p_1(\hat x;\hat w)^{y_i} \cdot p_0(\hat x;\hat w)^{(1-y_i)}] $$
Step 3.进行对数转换
然后即可在似然函数基础上对其进行(以e为底的)对数转换,为了方便后续利用优化方法求解最小值。此外,求解损失函数是下山问题,所以前面加负号。同样我们考虑构建负数对数似然函数: $$ \begin{aligned} L(\hat w) &= -ln(\prod^N_{i=1}[p_1(\hat x;\hat w)^{y_i} \cdot p_0(\hat x;\hat w)^{(1-y_i)}]) \ &= \sum^N_{i=1}[-y_i \cdot ln(p_1(\hat x;\hat w))-(1-y_i) \cdot ln(p_0(\hat x;\hat w))] \ &= \sum^N_{i=1}[-y_i \cdot ln(p_1(\hat x;\hat w))-(1-y_i) \cdot ln(1-p_1(\hat x;\hat w))] \end{aligned} $$
公式推导致此即可,后续我们将借助该公式进行损失函数求解。
Step 4.求解对数似然函数
通过数学推导可以证明,极大似然估计构建的逻辑回归损失函数是凸函数。因此,我们可以通过求偏导数等于0并联立方程组的方式求解参数。然而,这种方法在大规模数据中会涉及大量计算,不适用于复杂的数值运算。
在机器学习中,更常用的优化方法是梯度下降或牛顿法。其中,梯度下降是最为通用的求解损失函数的优化算法。下一节会搞梯度下降。
此外,还有一种推导逻辑回归损失函数的方法是通过KL散度,该方法引入了信息熵和交叉熵等概念。
交叉熵损失函数(参数估计)
先来搞明白熵的各种概念,然后构建损失函数并求解
熵、相对熵与交叉熵
接下来,我们介绍另一种构建逻辑回归损失函数的基本思路——借助相对熵(relative entropy,又称KL离散度)构建损失函数。尽管最终损失函数构建结果和极大似然估计相同,但该过程所涉及到的关于信息熵(entropy)、相对熵等概念却是包括EM算法、决策树算法等诸多机器学习算法的理论基础。
熵(entropy)的基本概念与计算公式
通常我们用熵(entropy)来表示随机变量不确定性的度量,或者说系统混乱程度、信息混乱程度。熵的计算公式如下: $$ H(X) = -\sum^n_{i=1}p(x_i)log(p(x_i)) $$ 其中,$p(x_i)$表示多分类问题中第$i$个类别出现的概率,$n$表示类别总数,通常来说信息熵的计算都取底数为2,并且规定$log0=0$。举例说明信息熵计算过程,假设有二分类数据集1标签如下:
则信息熵的计算过程中$n=2$,令$p(x_1)$表示类别0的概率,$p(x_2)$表示类别1的概率(反之亦然),则 $$ p(x_1)=\frac{1}{4} \ p(x_2)=\frac{3}{4} $$ 则该数据集的信息熵计算结果如下: $$ \begin{aligned} H(X) &= -(p(x_1)log(p(x_1))+p(x_2)log(p(x_2))) \ &=-(\frac{1}{4})log(\frac{1}{4})-(\frac{3}{4})log(\frac{3}{4}) \end{aligned} $$ 同时,在二分类问题中,$n=2$且$p(x_1)+p(x_2)=1$,我们也可推导二分类的信息熵计算公式为: $$ H(X) = -p(x)log(p(x))-(1-p(x))log(1-p(x)) $$ 其中$p(x)$为样本标签为0或1的概率。
熵的基本性质
熵的计算结果在
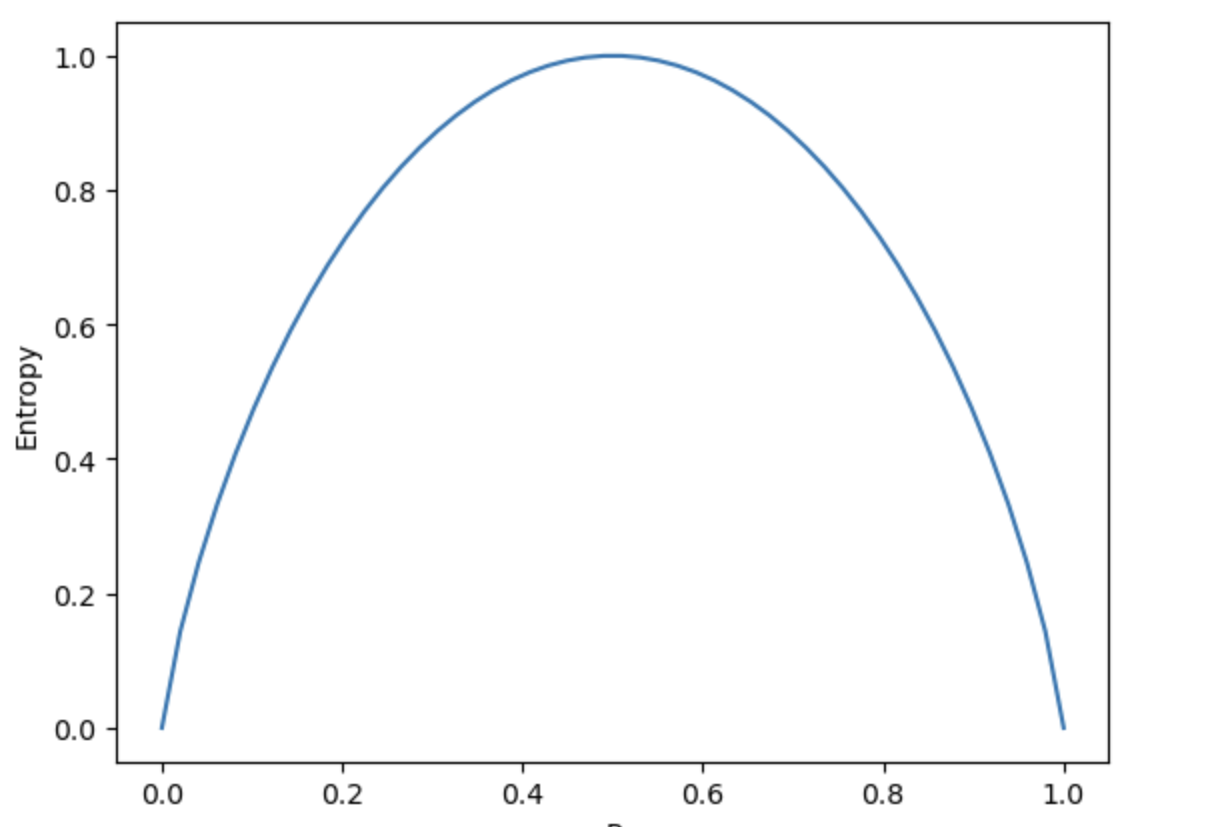
[0,1]之间,并且熵值越大,系统越混乱、信息越混乱。当标签取值不均时信息熵较高,标签取值纯度较高时信息熵较低。假设p为未分类数据集中1样本所占比例,则数据集信息熵随着p变化为变化趋势如下:
相对熵(relative entropy)与交叉熵(cross entropy)
相对熵也被称为Kullback-Leibler散度(KL散度)或者信息散度(information divergence)。通常用来衡量两个随机变量分布的差异性。假设对同一个随机变量X,有两个单独的概率分布P(x)和Q(x),当X是离散变量时,我们可以通过如下相对熵计算公式来衡量二者差异,和信息熵类似,相对熵越小,代表Q(x)和P(x)越接近。 $$ D_{KL}(P||Q)=\sum ^n_{i=1}P(x_i)log(\frac{P(x_i)}{Q(x_i)}) $$
从交叉熵的计算公式不难看出,这其实是一种非对称性度量,也就是$D_{KL}(P||Q)≠D_{KL}(Q||P)$。在机器学习领域,
Q为拟合分布P为真实分布,也被称为前向KL散度(forward KL divergence)。
上述相对熵公式等价于: $$ \begin{aligned} D_{KL}(P||Q)&=\sum ^n_{i=1}P(x_i)log(\frac{P(x_i)}{Q(x_i)}) \ &=\sum ^n_{i=1}P(x_i)log(P(x_i))-\sum ^n_{i=1}P(x_i)log(Q(x_i)) \ &=-H(P(x))+[-\sum ^n_{i=1}P(x_i)log(Q(x_i))] \end{aligned} $$ 而对于给定数据集,信息熵$H(P(X))$是确定的,因此相对熵的大小完全由$-\sum ^n_{i=1}P(x_i)log(Q(x_i))$决定。而该式计算结果也被称为交叉熵(cross entropy)。 $$ cross_entropy(P,Q) = -\sum ^n_{i=1}P(x_i)log(Q(x_i)) $$ 因此,如果我们希望P、Q二者分布尽可能接近,我们就需要尽可能减少相对熵,但由于相对熵=交叉熵-信息熵,而信息熵是一个固定值,因此我们只能力求减少交叉熵。
简单总结上述过程要点:
- 非对称性:KL散度是非对称的,即 $D_{KL}(P || Q) \neq D_{KL}(Q || P)$。
- 非负性:KL散度始终大于或等于零。只有在 P 和 Q 完全相同的情况下,KL散度才为零。
- 度量模型输出分布:交叉熵成为衡量模型输出分布接近真实分布的重要度量方法。。
交叉熵损失函数
交叉熵计算
例如有数据集情况如下:
| index | labels | predicts |
|---|---|---|
| 1 | 1 | 0.8 |
| 2 | 0 | 0.3 |
| 3 | 0 | 0.4 |
| 4 | 1 | 0.7 |
我们可以将其改写成如下形式:
| index | labels | predicts | 0类别 | 1类别 |
|---|---|---|---|---|
| 1 | 1 | 0.8 | 0.2 | 0.8 |
| 2 | 0 | 0.3 | 0.3 | 0.7 |
| 3 | 0 | 0.4 | 0.4 | 0.6 |
| 4 | 1 | 0.7 | 0.3 | 0.7 |
其中0类、1类表示每条样本可能所属的类别。围绕该数据集,****计算过程如下: $$ cross_entropy = -0 * log(0.2)-1*log(0.8) $$
。例如上述数据集,整体交叉熵计算结果为:$$ \frac{-1 * log(0.8) -1 * log(0.7) -1 * log(0.6) -1 * log(0.7)}{4} = 0.5220100086782713 $$ 据此,我们可以给出多样本交叉熵计算公式如下: $$ cross_entropy = -\frac{1}{m}\sum ^m_j \sum^n_ip(p_{ij})log(q_{ij}) $$ 其中m为数据量,n为类别数量。
对比极大似然估计函数
围绕上述数据集,如果考虑采用极大似然估计来进行计算,我们发现基本计算流程保持一致: $$ L(\hat w)= \sum^N_{i=1}[-y_i \cdot ln(p_1(\hat x;\hat w))-(1-y_i) \cdot ln(1-p_1(\hat x;\hat w))] $$ 带入数据可得: $$ -ln(0.8)-ln(0.7)-ln(0.6)-ln(0.7) = 1.4473190629576653 $$ 尽管具体数值计算结果有所差异,但基本流程都是类似的——取类别1的概率的对数运算结果进行累加再取负数。因此在实际建模过程中,考虑采用极大似然估计构建损失函数,和采用交叉熵构建损失函数,效果是相同的,二者构建的损失函数都能很好的描绘模型预测结果和真实结果的差异程度。
二分类交叉熵损失函数
据此,我们也可最终推导二分类交叉熵损失函数计算公式,结合极大似然估计的计算公式和交叉熵的基本计算流程,二分类交叉熵损失函数为: $$ binaryCE(\hat w)= -\frac{1}{n}\sum^N_{i=1}[y_i \cdot log(p_1(\hat x;\hat w))+(1-y_i) \cdot log(1-p_1(\hat x;\hat w))] $$ 在下一节,我们将介绍一种更加通用的求解损失函数的优化算法——梯度下降。并最终完成逻辑回归的参数求解。
到目前为止,构建损失函数的思路
- ,是的差异越小越好,从而获得最佳的参数
- 比如线性模型,以SSE作为损失函数
- ,使得这个概率越大越好,从而获得最佳参数
- 比如逻辑回归模型,用交叉熵或极大似然估计来表达预测正确的概率