Hong's External Brain

Appearance

本节内容 ​

  • 矩阵运算与线代基础

  • 矩阵求导基本方法

  • 最小二乘法基本理论

矩阵运算基础与线代基础 ​

在进入到本节正式内容之前，我们需要先补充一些矩阵相关基础概念，以及矩阵运算的基本方法。

在机器学习基础阶段，需要掌握的矩阵及线性代数基本理论包括：

  • 矩阵的形变及特殊矩阵的构造方法：包括矩阵的转置、对角矩阵的创建、单位矩阵的创建、上/下三角矩阵的创建等；
  • 矩阵的基本运算：包括矩阵乘法、向量内积、矩阵和向量的乘法等；
  • 矩阵的线性代数运算：包括矩阵的迹、矩阵的秩、逆矩阵的求解、伴随矩阵和广义逆矩阵等；
  • 矩阵分解运算：特征分解、奇异值分解和SVD分解等。
    本节将先介绍前三部分内容，矩阵分解部分内容将在后续补充。

1.NumPy中的矩阵表示 ​

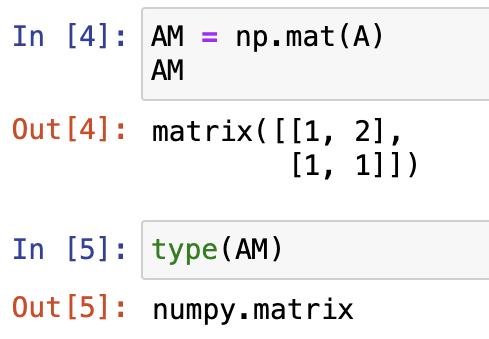
在NumPy中，二维数组(array)和matrix类型对象都可以用于表示矩阵，并且也都具备矩阵的代数学方法。

  • np.array
    • image-20240915141442543
  • np.mat
    • image-20240915141524109

关于两种对象类型的选取，此处进行简单说明：

  • np.mat对象和np.array对象底层基本结构不同
    • NumPy中的np.mat对象和MATLAB中的matrix类型等价
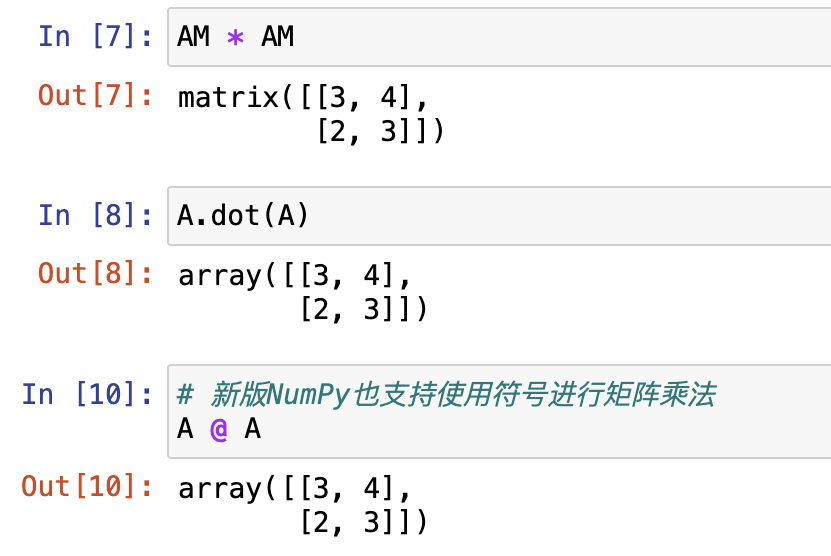
  • np.array对象的计算速度要快于np.mat对象；
  • np.mat对象可以通过运算符直接进行矩阵乘法，而np.array对象要进行矩阵乘法（及其他矩阵运算），则必须要使用包括linalg（线性代数运算）模块在内的相关函数。
    • image-20240915142037102

2.NumPy中特殊矩阵构造方法 ​

在实际线性代数运算过程中，经常涉及一些特殊矩阵，如单位矩阵、对角矩阵等，相关创建方法如下：

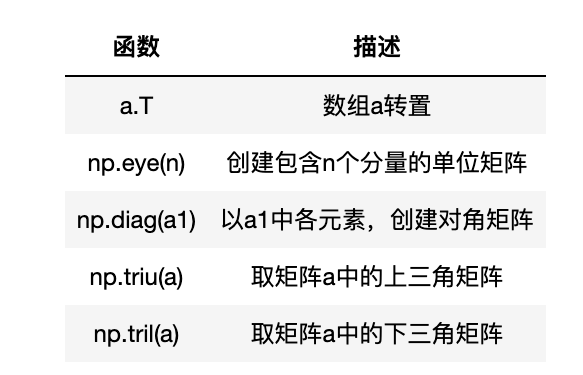
image-20240915142339677

创建矩阵 ​

image-20240915142700158

转置 ​

矩阵的转置就是每个元素行列位置互换

image-20240915142806432

创建单位矩阵 ​

单位矩阵和任何矩阵相乘，都将返回原矩阵。

image-20240915142856809

创建对角矩阵 ​

image-20240915143200102

偏移对角矩阵 ​

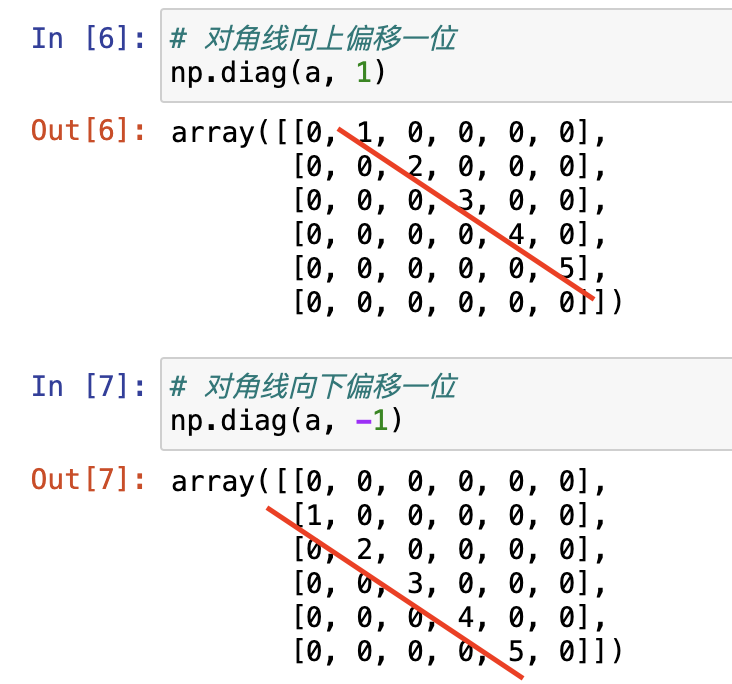
image-20240915143450931

取三角矩阵 ​

  • 取上三角矩阵**np.triu**: "Triangular Upper" 的缩写，表示 "上三角"。

    • 偏移：清0的位置相应得偏移
    image-20240915144302549

  • 取下三角矩阵**np.tril**: "Triangular Lower" 的缩写，表示 "下三角"。

    image-20240915143816672

3.NumPy中矩阵基本运算 ​

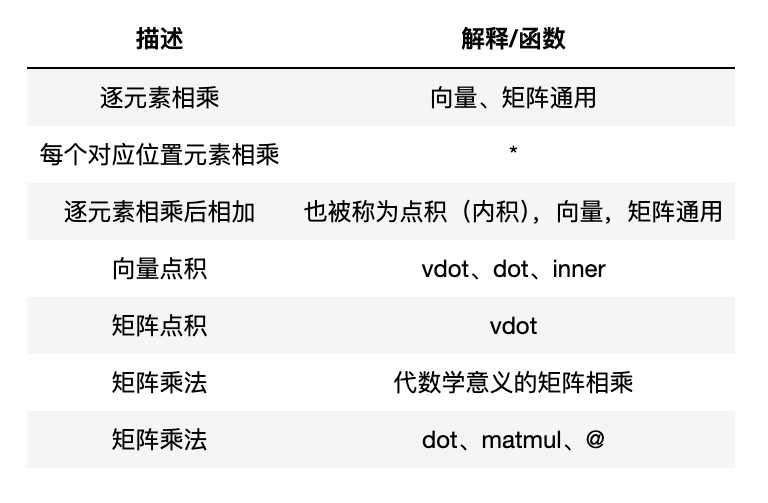
image-20240915144615486

逐元素相乘 ​

image-20240915144726308

向量点积 ​

所谓点积（也被称为内积），指的是向量或矩阵对应位置元素相乘后相加。

  • 向量点积有三种实现方法，
    • np.vdot
    • np.dot
    • np.ineer
image-20240915145233982

矩阵点积 ​

  • 矩阵点积：只有 np.vdot一种方法实现
    • np.vdot 的英文缩写是 "Vector Dot"
image-20240915145401128

矩阵乘法 ​

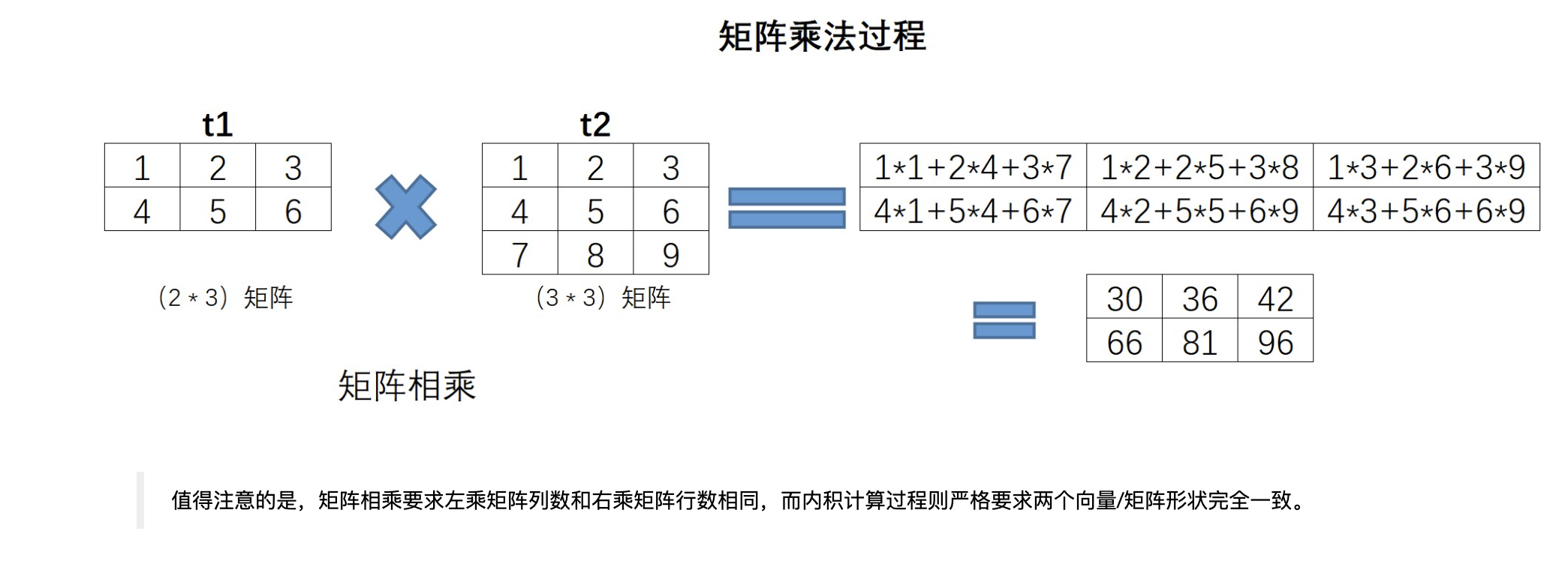
image-20240915150151026

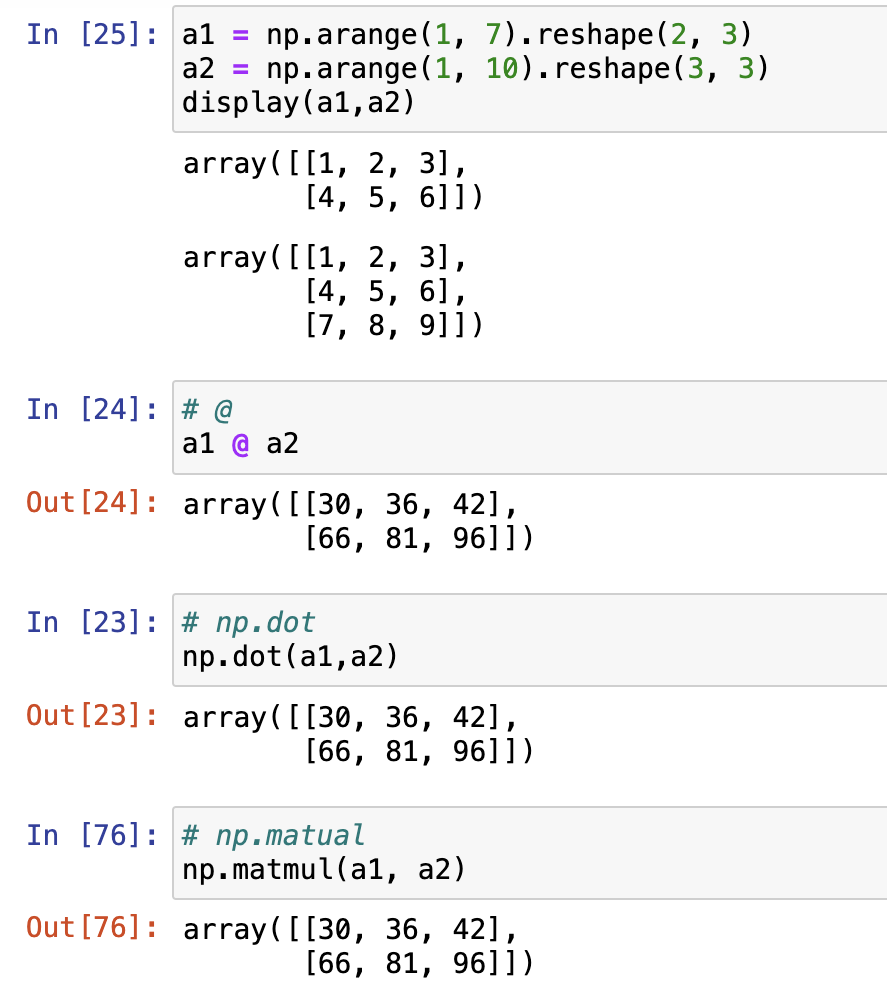
我们可以使用诸多方法实现矩阵乘法，包括：

  • np.dot
  • @
  • np.matmul
image-20240915150052320

4.NumPy中矩阵代数运算 ​

如果说矩阵的基本运算是矩阵基本性质，那么矩阵的线性代数运算，则是我们利用矩阵数据类型在求解实际问题过程中经常涉及到的线性代数方法，具体相关函数如下：

image-20240915150327210

在 NumPy 中，numpy.linalg 是 "linear algebra"（线性代数）的缩写。这个模块包含了许多线性代数相关的函数，比如矩阵分解、特征值计算、求逆等。你可以使用 numpy.linalg 来进行这些常见的线性代数操作。

矩阵的迹（trace） ​

矩阵的迹（trace）是矩阵的对角线元素的总和。对于一个 $n \times n$的方阵 $A$，其迹定义为：

$\text{trace}(A) = \sum_{i=1}^{n} A_{ii}$

image-20240915150723740

如果矩阵为非方阵矩阵时，将其截取为最小的方阵是一种常见的方法，以便计算迹。

具体来说，如果矩阵A的尺寸是 $m \times n$（其中 $m \neq n$），你可以截取出一个$\min(m, n) \times \min(m, n)$的子矩阵，然后计算这个方阵的迹。以下是详细步骤：

  1. 确定子矩阵的大小：选择矩阵 $A$ 的前$min(m, n)$ 行和前$\min(m, n)$ 列，形成一个方阵。
  2. 计算迹：对这个方阵计算迹。

矩阵的秩 ​

矩阵的秩(rank)：线性独立行（列）的最大数量

  • 举个例子，下图的矩阵秩为2 即r=2
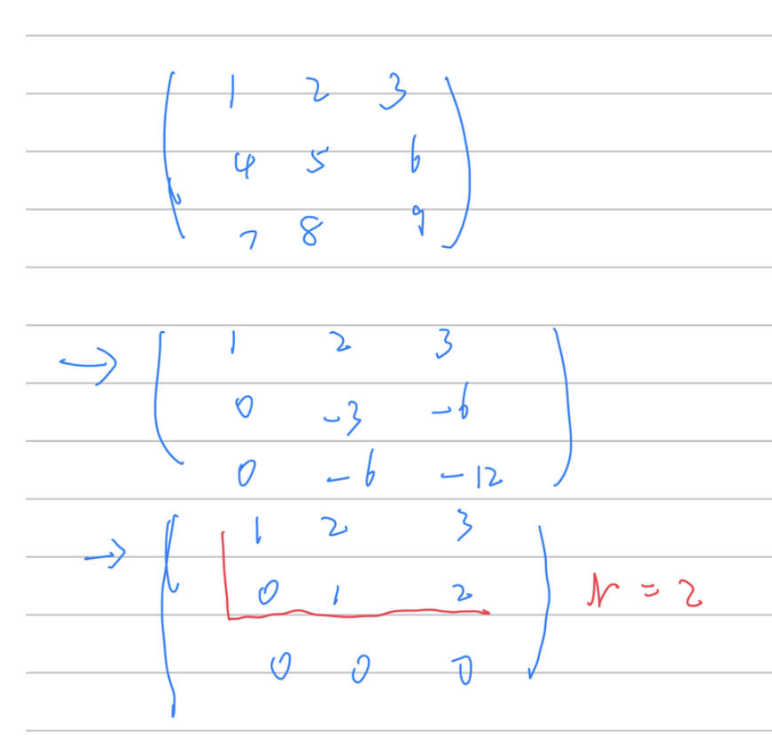
image-20240915152027975
  • np.linalg.matrix_rank()求解矩阵的秩
image-20240915152318757

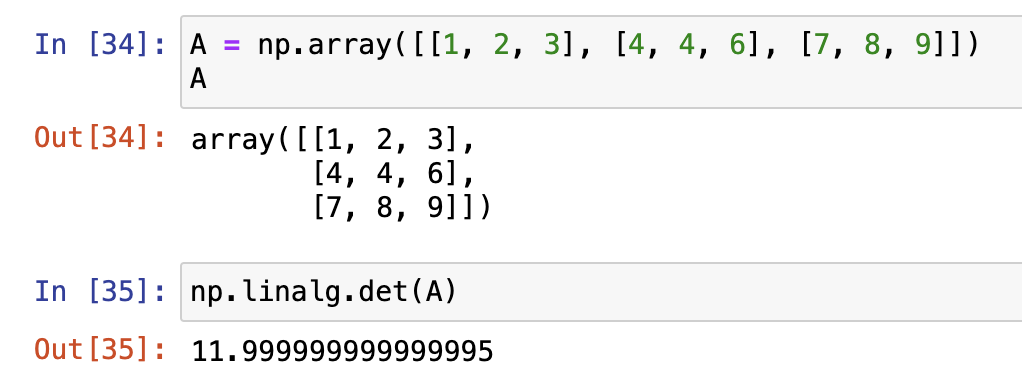
矩阵的行列式(det) ​

所谓行列式，我们可以简单将其理解为矩阵的一个基本性质或者属性，通过行列式的计算，我们能够知道

  • 矩阵是否可逆
    • 如果$\text{det}(A) \neq 0$，那么矩阵 $A$ 是可逆的；
    • 如果$\text{det}(A) = 0$，则矩阵 $A$ 是奇异的（即不可逆）。
  • 矩阵是否满秩
    • 对于一个$n \times n$ 方阵，如果行列式不为零，则矩阵的秩为 $n$，即矩阵满秩。
    • 对于一个$n \times n$ 方阵，如果行列式为零，则矩阵的秩小于$n$，即矩阵不满秩。

从而可以进一步求解矩阵所对应的线性方程。

np.linalg.det()计算det

image-20240915160243515

矩阵的逆 ​

对于满秩的方正来说，可以求其逆矩阵。从基本定义上来看，如果矩阵B和矩阵A相乘能够得到单位矩阵，即： $$ B \cdot A = E $$ 则称B为A的逆矩阵，也可将B写作$A^{-1}$。当然，逆矩阵的性质是相互的，我们也可称A为B的逆矩阵，或者A和B互为逆矩阵。

  • 使用np.linalg.inv()求逆矩阵

    • inv()是inverse的缩写
    image-20240915161308901

矩阵在优化算法中的应用 ​

在铺垫了基本矩阵和线性代数相关知识后，接下来，我们尝试将Lesson 1中的方程组表示形式转化为矩阵表示形式，并借助矩阵方法进行相关方程的求解。并且，在Lesson 1中，我们已经简单讨论了最小二乘法这一优化算法的基本思路，最小二乘法一个最基础的优化算法，无论是其背后的数学推导还是实际应用，都值得继续深究。因此，本节开始，我们先从矩阵方程入手，先进行矩阵运算的相关方法的回顾、以及进行矩阵求导方法的讲解，再从一个更加严谨的数学角度出发，讨论最小二乘法的基本原理。

1.矩阵方程求解 ​

在Lesson 1中，我们曾经利用损失函数的偏导函数方程组进行简单线性回归模型参数的求解： $$ \frac{\partial{SSELoss}}{\partial{(w)}}
= 2(2-w-b)(-1) + 2(4-3w-b)(-3)\ = 20w+8b-28 \ = 0 $$

$$ \frac{\partial{SSELoss}}{\partial{(b)}}
= 2(2-w-b)(-1) + 2(4-3w-b)(-1)\ = 8w+4b-12 \ = 0 $$

像上面这样通过求损失函数偏导的方式求解损失函数最小值，虽然可以，但如果想提高计算效率，借助编程工具求解上述方程组，则需要将原先的方程组求解问题转化为矩阵方程的求解问题。

矩阵方程的具体求解如下：

如上述所示，损失函数求偏导后的方程组为： $$ 20w+8b-28=0 \ 8w+4b-12=0 $$ 首先将其转化为矩阵方程问题，则令： $$ A = \left [\begin{array}{cccc} 20 &8 \ 8 &4 \ \end{array}\right] $$

$$ B = \left [\begin{array}{cccc} 28 \ 12 \ \end{array}\right] $$

$$ X = \left [\begin{array}{cccc} w \ b \ \end{array}\right] $$

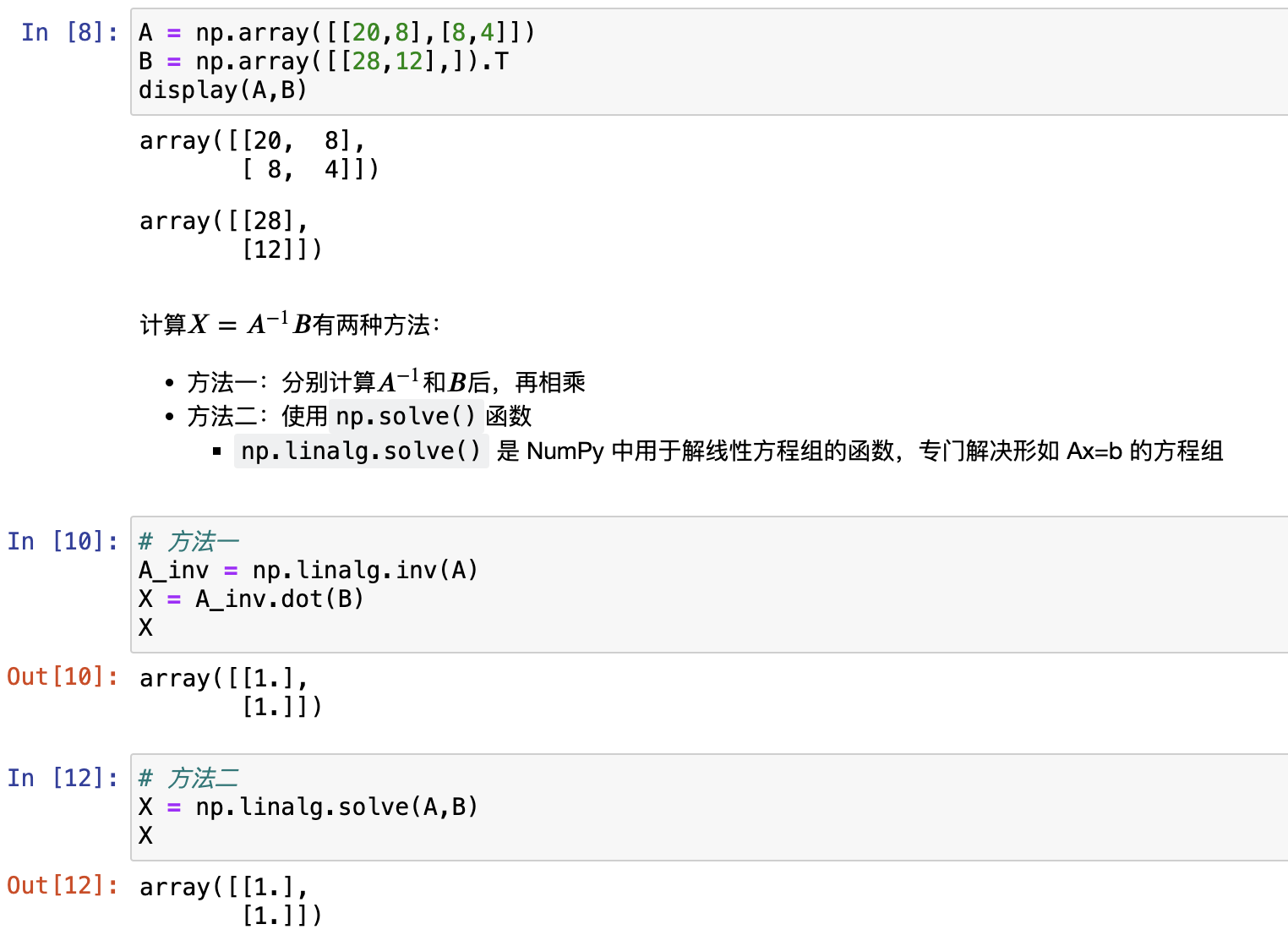
其中$X$为参数向量。借助矩阵运算相关知识，上述方程组可等价表示为： $$ A \cdot X - B = 0 $$ 即 $$ A \cdot X = B $$ 至此我们就将方程组转化为了矩阵方程，并且，借助矩阵运算，我们可以直接在矩阵方程中对参数向量$X$进行求解。首先我们利用NumPy基础知识，通过创建二维张量去表示上述矩阵方程中的A和B

即 $$ X=A^{-1}B $$ 计算$X=A^{-1}B$有两种方法：

  • 方法一：分别计算$A^{-1}$和$B$后，再相乘
  • 方法二：使用np.solve()函数
    • np.linalg.solve() 是 NumPy 中用于解线性方程组的函数，专门解决形如 Ax=b 的方程组
image-20240915201551627

所以 $$ X = \left [\begin{array}{cccc} w \ b \ \end{array}\right] =\left [\begin{array}{cccc} 1 \ 1 \ \end{array}\right] $$

2.向量求导运算 ​

在上面的矩阵方程求解的演示中，使用的是损失函数求偏导后的方程组 $$ 20w+8b-28=0 \ 8w+4b-12=0 $$ 那么如果用矩阵的形式表示损失函数，矩阵方程形式的损失函数如何求导？

在这之前先补充向量求导和矩阵求导的基础知识

向量求导的定义法 ​

向量求导的定义法，也称为向量的梯度（gradient），是

设$f(x)$是一个关于$x$的函数，其中$x$是向量变量，并且 $$ x = [x_1, x_2,...,x_n]^T $$ 则 $$ \frac{\partial f}{\partial x} = [\frac{\partial f}{\partial x_1}, \frac{\partial f}{\partial x_2}, ..., \frac{\partial f}{\partial x_n}]^T $$

值得注意的是，多元函数是一定能够求得梯度向量的，但梯度向量或者说向量求导结果，能否由一些已经定义的向量解决表示，如𝐴A就是𝑓(𝑥)f(x)的向量求导结果，则不一定。

向量求导可以视作矩阵求导的一种特殊形式。

矩阵求导 ​

  1. $$ \frac{\partial A}{\partial x} = 0 $$

  2. $$ \frac{\partial(x^T \cdot A)}{\partial x} = \frac{\partial(A^T \cdot x)}{\partial x} = A $$

  3. $$ \frac{\partial (x^T \cdot x)}{\partial x} = 2x $$

  4. $$ \frac{\partial (x^T A x)}{x} = Ax + A^Tx $$

上述求导公式的证明 ​

  • $$ \frac{\partial A}{\partial x} = 0 $$

  • $$ \frac{\partial(x^T \cdot A)}{\partial x} = \frac{\partial(A^T \cdot x)}{\partial x} = A $$

    • 证明：

    • $$ \begin{aligned} \frac{\partial(x^T \cdot A)}{\partial x} & = \frac{\partial(A^T \cdot x)}{\partial x}\ & = \frac{\partial(a_1 \cdot x_1 + a_2 \cdot x_2 +...+ a_n \cdot x_n)}{\partial x}\ & = \left [\begin{array}{cccc} \frac{\partial(a_1 \cdot x_1 + a_2 \cdot x_2 +...+ a_n \cdot x_n)}{\partial x_1} \ \frac{\partial(a_1 \cdot x_1 + a_2 \cdot x_2 +...+ a_n \cdot x_n)}{\partial x_2} \ . \ . \ . \ \frac{\partial(a_1 \cdot x_1 + a_2 \cdot x_2 +...+ a_n \cdot x_n)}{\partial x_n} \ \end{array}\right] \ & =\left [\begin{array}{cccc} a_1 \ a_2 \ . \ . \ . \ a_n \ \end{array}\right] = A \end{aligned} $$

  • $$ \frac{\partial (x^T \cdot x)}{\partial x} = 2x $$

    • 证明

    • $$ \begin{aligned} \frac{\partial(x^T \cdot x)}{\partial x} & = \frac{\partial(x_1^2+x_2^2+...+x_n^2)}{\partial x}\ & = \left [\begin{array}{cccc} \frac{\partial(x_1^2+x_2^2+...+x_n^2)}{\partial x_1} \ \frac{\partial(x_1^2+x_2^2+...+x_n^2)}{\partial x_2} \ . \ . \ . \ \frac{\partial(x_1^2+x_2^2+...+x_n^2)}{\partial x_n} \ \end{array}\right] \ & =\left [\begin{array}{cccc} 2x_1 \ 2x_2 \ . \ . \ . \ 2x_n \ \end{array}\right] = 2x \end{aligned} $$

    • 此处$x^Tx$也被称为向量的交叉乘积(crossprod)。

  • $$ \frac{\partial (x^T A x)}{x} = Ax + A^Tx \ 其中A是一个(nn)的矩阵，A_{nn}=(a_{ij})_{a=1,j=1}^{n,n} $$

    • 证明

image-20240915210530604

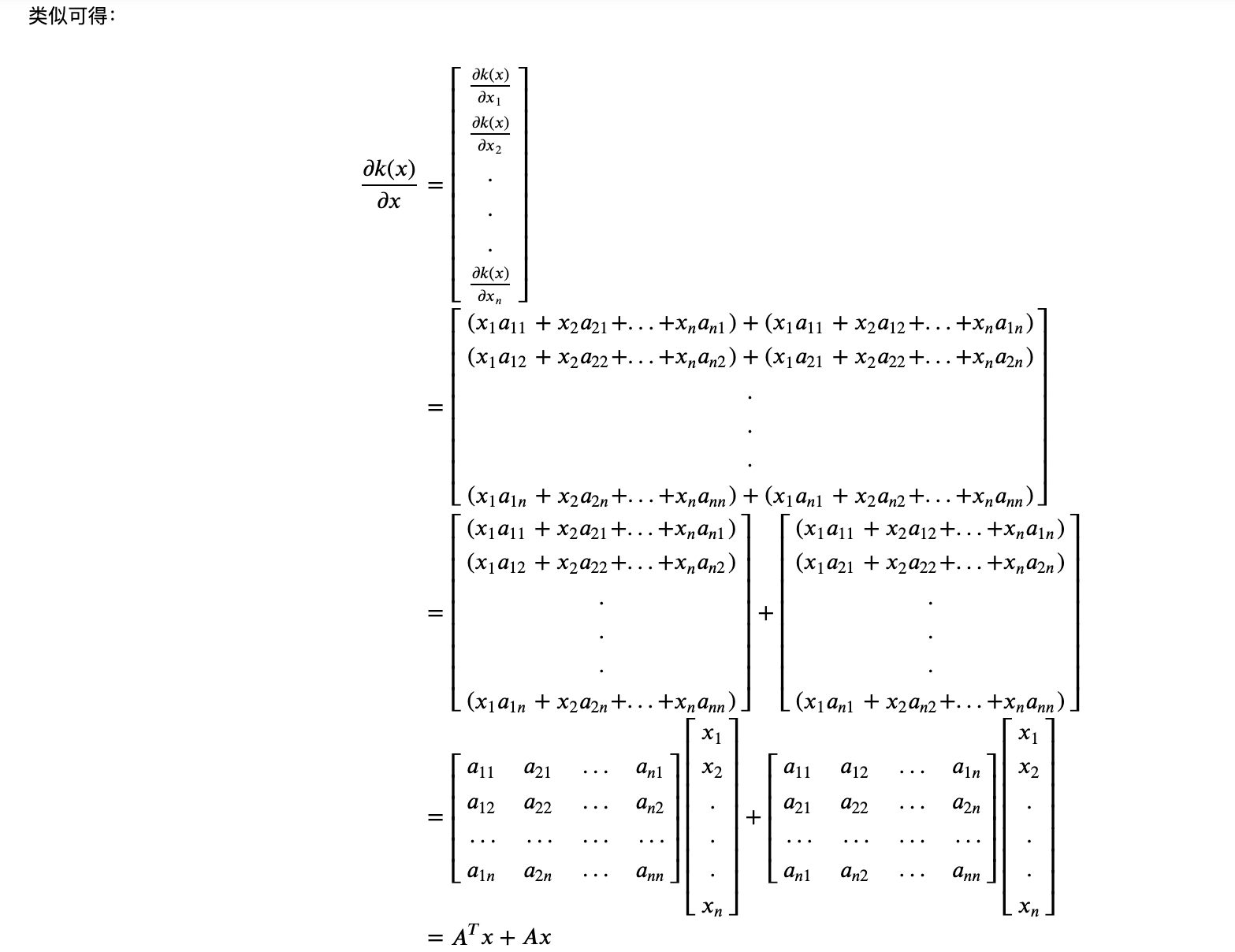
image-20240915210439833

矩阵求导公式速查 ​

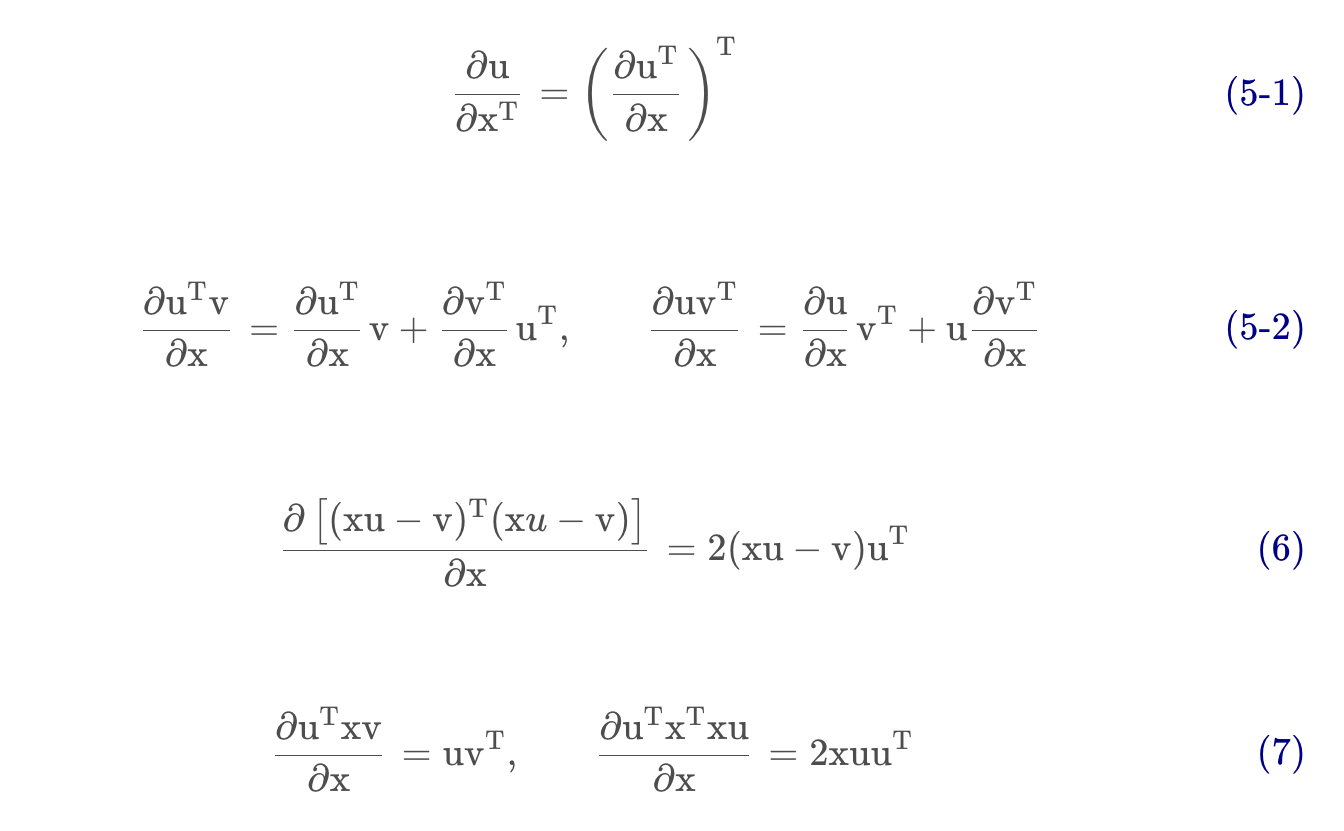
image-20240915211941992image-20240915212010590image-20240915212052209

矩阵方程和矩阵函数的区别 ​

  • 矩阵方程

    • 定义： 矩阵方程是一种涉及未知矩阵的等式，其中矩阵的运算（如加法、乘法）和常数矩阵参与其中。

    • 形式： 一般形式为$AX = B$ 或 $X A = B$，其中$ A$、$B$是已知矩阵，$X$ 是待求解的未知矩阵。

  • 矩阵函数

    • 定义： 矩阵函数是对矩阵应用的函数，结果通常也是一个矩阵。矩阵函数包括对矩阵的各种运算（如矩阵的幂、矩阵的指数、对数等）。

    • 形式： 一般形式为$f(A)$，其中 $f$是定义在矩阵上的函数，$A$ 是矩阵。

最小二乘法基本理论（得手写能算出来） ​

有了上述内容铺垫之后，接下来，我们从数学角度讨论最小二乘法的基本理论。

并尝试简单实现最小二乘法求解损失函数的一般过程。

  • Step1：模型及方程组的矩阵形式改写
  • Step2：构造损失函数
  • Step3：使用最小二乘法求解损失函数
  • Step4：最小二乘法的简单实现

step 1:模型及方程组的矩阵形式改写 ​

首先，我们尝试对模型进行矩阵形式改写。

原来多元线性回归的模型如下： $$ f(x) = w_1x_1+w_2x_2+...+w_dx_d+b $$

令 $$ w = [w_1,w_2,...w_d]^T \ x = [x_1,x_2,...x_d]^T $$ 则模型可以改写成： $$ f(x) = w^Tx+b $$

在机器学习领域，我们将线性回归自变量系数命名为w，其实是weight的简写，意为自变量的权重。

然后考虑将数据带入改写后的方程里，假设现在总共有m条观测值，$x^{(i)} = [x_1^{(i)}, x_2^{(i)},...,x_d^{(i)}]$，则带入模型可构成m个方程： $$ \left [\begin{array}{cccc} w_1x_1^{(1)}+w_2x_2^{(1)}+...+w_dx_d^{(1)}+b \ w_1x_1^{(2)}+w_2x_2^{(2)}+...+w_dx_d^{(2)}+b \ . \ . \ . \ w_1x_1^{(m)}+w_2x_2^{(m)}+...+w_dx_d^{(m)}+b \ \end{array}\right] ​

\left [\begin{array}{cccc} \hat y_1 \ \hat y_2 \ . \ . \ . \ \hat y_m \ \end{array}\right] $$ 截距$b$看着很不爽，继续改写

令 $$ \hat w = [w_1,w_2,...,w_d,b]^T \ \hat x = [x_1,x_2,...,x_d,1]^T $$ 当将$x$的m条数据带入后，$\hat X$向量变为: $$ \hat X = \left [\begin{array}{cccc} x_1^{(1)} &x_2^{(1)} &... &x_d^{(1)} &1 \ x_1^{(2)} &x_2^{(2)} &... &x_d^{(2)} &1 \ ... &... &... &... &1 \ x_1^{(m)} &x_2^{(m)} &... &x_d^{(m)} &1 \ \end{array}\right] $$

$$ y = \left [\begin{array}{cccc} y_1 \ y_2 \ . \ . \ . \ y_m \ \end{array}\right] $$

其中

  • $\hat w$：方程系数所组成的向量，并且我们将自变量系数和截距放到了一个向量；
  • $\hat x$：方程自变量和1共同组成的向量；
  • $\hat X$：样本数据特征构成的矩阵，并在最后一列添加一个全为1的列；
  • $y$：样本数据标签所构成的列向量;
  • $\hat y$：预测值的列向量。

因此模型的方程可以表现为： $$ f(\hat x) = \hat w^T \cdot \hat x $$

Step2：构造损失函数 ​

在方程组的矩阵表示基础上，我们这里以SSE作为多元线性回归模型的损失函数为例，基于计算流程构建关于𝑤̂的损失函数： $$ SSELoss(\hat w) = ||y - X\hat w||_2^2 = (y - X\hat w)^T(y - X\hat w) $$

值得注意的是这里损失值的计算采用了L2范数$ ||y - X\hat w||_2^2$，因此补充一下什么是向量的L2范数

向量的L2范数：是向量各分量平方和的平方根，例如，向量 $\mathbf{v} = [3, 4]$的L2范数为：

$|\mathbf{v}|_2 = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5$

L2 范数等于点积的平方根：$|\mathbf{a}|_2 = \sqrt{a^T \cdot a} $

向量的L1范数：是向量中各个元素绝对值的总和。例如，假设 $\mathbf{v} = [3, -4, 1]$，则其L1范数为：

$|\mathbf{v}|_1 = |3| + |-4| + |1| = 3 + 4 + 1 = 8$

Step3：使用最小二乘法求解损失函数 ​

在确定损失函数的矩阵表示形式之后，接下来即可利用最小二乘法进行求解。其基本求解思路仍然和Lesson 0中介绍的一样，先求导函数、再令导函数取值为零，进而解出参数取值。只不过此时求解的是矩阵方程。

在此之前，补充两个矩阵转置的规则： $$ (A-B)^T=A^T-B^T \ (AB)^T=B^TA^T $$ 接下来，对$SSELoss(w)$求导并令其等于0： $$ \begin{aligned} \frac{SSELoss(\hat w)}{\partial{\boldsymbol{\hat w}}} &= \frac{\partial{||\boldsymbol{y} - \boldsymbol{X\hat w}||_2}^2}{\partial{\boldsymbol{\hat w}}} \ &= \frac{\partial(\boldsymbol{y} - \boldsymbol{X\hat w})^T(\boldsymbol{y} - \boldsymbol{X\hat w})}{\partial{\boldsymbol{\hat w}}} \ & =\frac{\partial(\boldsymbol{y}^T - \boldsymbol{\hat w^T X^T})(\boldsymbol{y} - \boldsymbol{X\hat w})}{\partial{\boldsymbol{\hat w}}}\ &=\frac{\partial(\boldsymbol{y}^T\boldsymbol{y} - \boldsymbol{\hat w^T X^Ty}-\boldsymbol{y}^T\boldsymbol{X \hat w} +\boldsymbol{\hat w^TX^T}\boldsymbol{X\hat w})}{\partial{\boldsymbol{\hat w}}}\ & = 0 - \boldsymbol{X^Ty} - \boldsymbol{X^Ty}+X^TX\hat w+(X^TX)^T\hat w \ &= 0 - \boldsymbol{X^Ty} - \boldsymbol{X^Ty} + 2\boldsymbol{X^TX\hat w}\ &= 2(\boldsymbol{X^TX\hat w} - \boldsymbol{X^Ty}) = 0 \end{aligned} $$ 即 $$ X^TX\hat w = X^Ty $$ 参数为$w$，因此$w$为： $$ \hat w = (X^TX)^{-1}X^Ty $$

Step4：最小二乘法的简单实现 ​

接下来，我们回到最初的例子，简单尝试利用上述推导公式求解简单线性回归参数。原始数据如下：

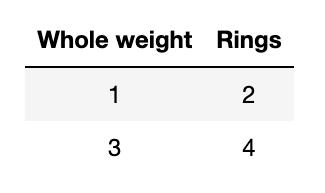
image-20240916115048572

因此利用矩阵表达式，可进行如下形式的改写：

特征矩阵： $$ \hat X =
\left [\begin{array}{cccc} 1 &1 \ 3 &1 \ \end{array}\right] $$ 标签数组： $$ y = \left [\begin{array}{cccc} 2 \ 4 \ \end{array}\right] $$ 参数向量： $$ \hat w = \left [\begin{array}{cccc} w \ b \ \end{array}\right] $$ 求解公式为： $$ \begin{aligned} \hat w &= (X^TX)^{-1}X^Ty \ &= (\left [\begin{array}{cccc} 1 &1 \ 3 &1 \ \end{array}\right]^{T} \left [\begin{array}{cccc} 1 &1 \ 3 &1 \ \end{array}\right])^{-1} \left [\begin{array}{cccc} 1 &1 \ 3 &1 \ \end{array}\right]^{T} \left [\begin{array}{cccc} 2 \ 4 \ \end{array}\right] \ \end{aligned} $$ 代码实现过程：

image-20240916115229080

即解得$w=1,b=1$，即模型方程为$y=x+1$。至此，我们即完成了最小二乘法的推导以及简单实现。其中，相比于记忆最终最小二乘法求解损失函数的计算公式，更加重要的是理解并掌握矩阵表示方程组的方法以及矩阵求导计算方法。

np.linalg.lstsq() ​

最小二乘法计算函数，通过该方法，我们能够在直接输入特征矩阵和标签数组的情况下进行最小二乘法的计算，并在得出最小二乘法计算结果的同时，也得到一系列相应的统计指标结果。

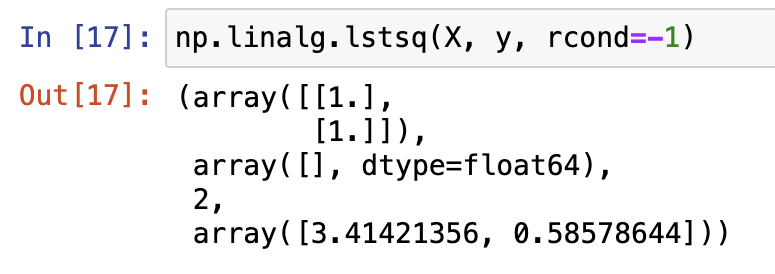
image-20240916120050956

返回的元组中：

  • solution: 参数向量
  • residuals: SSE，返回空数组就意味着SSE=0
  • rank: 矩阵 $A$ 的秩。
  • singular_values: 矩阵$ A$ 的奇异值，用于评估数值稳定性。

最小二乘法的局限性 ​

  • 矩阵不可逆性

    • 最小二乘法的解析解公式为：$\hat w = (X^TX)^{-1}X^Ty $
    • 这个公式成立的前提是矩阵$X^T X$必须是可逆的。如果不可逆，最小二乘法也不成立

  • 计算效率

    • 计算复杂度：计算 $(X^T X)^{-1}$的时间复杂度为 $O(p^3)$，其中 $p$ 是特征的数量。当特征数量非常大时，计算效率较低。