本节内容和上节回顾

• 机器学习基本概念补充
• 手动线性回归实验
• 机器学习基本流程

上节回顾

机器学习模型训练相关核心概念：

• 模型评估指标：用于评估模型实际效果的数值型指标，如准确率；

• 模型参数：对模型最终输出结果有影响的模型关键指标，如自变量加权求和汇总过程中的权重；

• 模型训练：指通过不断的数据输入、模型参数得到有效调整的过程，此处模型参数的有效调整指的是调整之后能够提升模型表现。

机器学习概念补充

经典统计分析与机器学习概念的区别

线性回归模型是诞生于是统计学领域的一类模型，同时也是整个线性类模型大类的基础模型，是一类非常重要的统计学模型。在经典统计学领域，线性回归模型拥有坚实的数学理论基础作为支撑，曾在很长一段时间内都是数理统计分析建模最通用的模型之一。

不过，值得一提的是，使用传统的统计学方法构建线性回归模型其实并不简单，如果要构建一个统计学意义的线性回归模型，则我们至少需要掌握随机变量的基本分布、变量相关性与独立性、方差分析等基本统计学知识，才能够上手构建线性回归模型。

而在机器学习领域，由于机器学习的基本建模思路和流程和经典统计分析有很大区别，在构建线性回归模型时流程较为简单，外加线性回归模型本身可解释性较强，因此可以作为入门的第一个算法来学习。

其实，从发展历程上来看，有关“算法”或者“模型”的概念早已有之，而实际作用和机器学习算法类似的，就是经典统计学领域的统计分析类算法。不过，尽管机器学习算法是统计分析算法目标一致——核心都是围绕某个具体目标、尝试进行有效的预测，但二者的建模流程和基本思路却有着天壤之别。更多关于二者区别的介绍，我们将在后续课程中逐渐展开讨论。

当然，从学术角度考虑，机器学习是否属于统计学尚存争论。课上不作过多学术讨论，此处所谓机器学习和统计方法之间的区别，特指与经典统计分析方法（尤其是遵循古典假设的统计学模型）之间的区别。

从机器学习的角度出发，所谓线性回归，指的是自变量（特征）加权求和汇总求得因变量（标签）的过程。例如Lesson 0中$y=w1x1+w2x2$的计算过程，就是一个简单的线性回归。当然，此处我们还需补充关于机器学习中和数据相关的基本概念。

数据与数据集相关概念

数据与数据集

• 数据是信息的集合，通常是对事物、现象、事件的测量或记录。它可以是单个值，也可以是多个值的组合。

• 数据集是按某种结构组织起来的多个数据点的集合。一个数据集通常由多条记录（或样本）组成，每条记录可能包含多个属性（或特征）。数据集通常用于分析、建模和训练机器学习算法。

特征与标签

• **特征：**是用于描述样本的一些变量或属性。
• **标签：**是你要预测的目标变量。

一般来说，标签列需要放在最后一列。

注意：数据集中的列也被称为字段，鸢尾花数据集中总共有5列，也就总共有5个字段。

不同时代的数据集

下一节的手动线性回归实验**使用了鸢尾花数据集（iris datasets）和鲍鱼数据集(abalone datasets)。这些数据集通常用于机器学习入门，因为它们经过精心统计，数据质量较高。

在过去，数据大多通过手工测量和记录，因此数据量小但质量高，经典统计学方法正是在这种背景下发展起来的。

机器学习的广泛应用和对数据质量要求较低的特性，使其在“大数据时代”成为最普适的算法。

当然，也正因如此，我们后续也不会大规模使用一些数据质量特别高、建模门槛比较低的数据集。实际上，在后续的课程中，我们将主要是用三类数据集去进行三个层次的教学。其一是手动创建的、具备一定规律和难度可自定义的数据集，用于前期训练，其二则是竞赛数据，用于综合训练，其三则是企业案例数据，结合实际应用情况进行建模。

连续变量与离散变量

• 连续变量：是指可以取无限多个值的变量。它们通常是可以测量的数值，在给定范围内的任意值都可能存在。这些值之间没有间隙，可以是小数或任意精度的数值。
• 离散变量是指只能取有限个或可数的值的变量，通常是整数或分类值。这些值之间有明确的间隔，不能是小数。
  • • **名义变量：**指的是随机变量取得不同离散值时，取值大小本身没有数值意义，只有指代意义。例如，用0/1代表男女，则该变量没有1>0的数值意义。
    • **顺序变量：**则有大小方面的数值意义，例如使用0/1/2代表高中/本科/研究生学历，则可用2>1>0来表示学习的高低之分。

模型类型

分类问题与回归问题

• 分类问题
  • 分类问题的目标是将输入数据分配到离散的类别或标签中。换句话说，分类模型的输出是有限的、离散的类别
  • 此时对应的模型就是分类模型
  • 分类模型专注于区分不同类别，常用于识别、分类任务。
• 回归问题
  • 回归问题的目标是预测一个连续的数值输出。换句话说，回归模型的输出是一个连续的实数。
  • 此时对应的模型就是回归模型
  • 回归模型专注于预测连续数值，常用于价格预测、时间序列分析等任务。

手动线性回归实验

1.数据准备

因为是回归问题，所以使用鲍鱼数据集

2.模型准备

这里用最简单的回归模型做示范 $$ y = wx + b $$ 除此之外，线性模型还有以下的形式： $$ y = w_1x_1+w_2x+...+w_nx_n+b $$ 和 $$ y = w_1x_1^2+w_2x_2+b $$

3.线性回归模型训练

模型训练的本质：有方向的参数调整

在$y = wx + b$中，参数有两个：

• $w$
• $b$

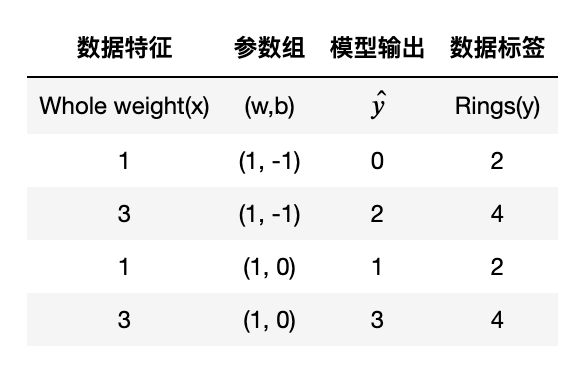
参数会大大影响模型输出结果，模型训练的本质就是找到模型回归或预测效果最好时的参数组合。那么问题来了，怎么知道模型的效果好不好那？用什么指标来量化？

模型评估指标和损失函数的异同

在学模型评估指标和损失函数之前，现搞清楚他俩的异同

损失函数和模型评估指标都是用于评估模型效果的重要工具，但它们的作用和应用场景有所不同。下面是它们的主要区别：

损失函数

• 目的: 衡量模型在训练过程中对数据的拟合程度。损失函数用于训练阶段， 在优化过程中，损失函数的值用于调整模型的参数，以使预测结果尽可能接近真实值。模型的训练目标是使损失函数的值最小化。

模型评估指标

• 目的: 在模型训练完成后，用于评估模型在测试集上的表现，以了解模型的实际效果。
• 功能: 评估指标用于模型的性能评估阶段，帮助比较不同模型或调整模型的超参数。它们提供了一种对模型进行性能评估的标准。

区别总结

1. 使用阶段:
   • 损失函数: 在训练过程中使用，优化模型的参数。
   • 评估指标: 在模型训练完成后使用，评估模型的效果。
2. 目标:
   • 损失函数: 最小化误差，指导模型参数的更新。
   • 评估指标: 评估模型的总体性能和效果，帮助选择最佳模型。
3. 应用:
   • 损失函数: 主要用于模型训练和优化。
   • 评估指标: 主要用于模型性能的报告和比较。

总的来说，损失函数是模型训练过程中的核心，而评估指标则是在模型训练后用于评估和比较模型效果的工具。

模型评估指标

模型评估指标是评估模型输出结果“好与坏”的标量计算结果，其最终结果一般由模型预测值$𝑦̂$ 和真实值$y$共同计算得出。

• 分类模型：分类模型的评估指标有多种选择，适用于不同的应用场景，特别是当类分布不平衡时，除了准确率之外，还需要考虑其他指标精确率（Precision），召回率（Recall），F1 Score。

• 回归模型：评估指标是残差平方和（SSE），均方误差（MSE），均方根误差（RMSE）

  • 残差平方和，指的是模型预测值$\hat y$和真实值$y$之间的差值的平方和，计算结果表示预测值和真实值之间的差距，结果越小表示二者差距越小，模型效果越好。

    • $$ SSE = \sum_{i=1}^{n}(\hat y_i-y_i)^2 $$

    • SSE越小，代表预测结果和真实结果的差异越小

  • 均方误差：就是在SSE的基础上除样本量，求平均

    • $$ \text{MSE} = \frac{1}{n} \sum_{i=1}^{n} (\hat{y}_i - y_i)^2 $$

  • 均方根误差（RMSE）：在MSE的基础上开平方，开平方可以恢复误差的单位

    • 恢复误差的单位： MSE 是通过对每个样本的误差平方再求均值得到的。因此，MSE 的单位是原始数据单位的平方。例如，如果目标变量 y 的单位是米（m），那么 MSE 的单位将是平方米（m²）。RMSE开根又恢复为米（m），使得衡量误差的指标解释性增强。

    • $$ \text{RMSE} = \sqrt{\frac{1}{n} \sum_{i=1}^{n} (\hat{y}_i - y_i)^2} $$

损失函数

和模型评估指标是真实值和预测值的计算过程不同，，基本计算过程如下：

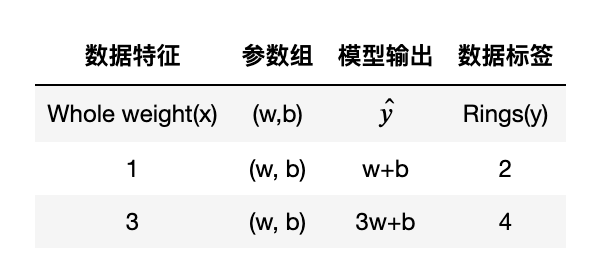$$ SSELoss(w, b) = (y_1 - ŷ_1)^2 + (y_2 - ŷ_2)^2 = (2 - w - b)^2 + (4 - 3w - b)^2 $$ **通过求解带有模型参数的函数的最小值，此时损失函数最小值对应的参数就是最优模型参数**。然后再使用模型评估指标来量化该参数下模型的效果。

利用最优化方法求解损失函数

现在已经知道只要求的损失函数的最小值所对应的参数就是模型的最优参数。

而求解损失函数最小值，分为两种情况：

• 有约束条件
• 无约束条件

利用优化方法求解损失函数最小值及其取得最小值时损失函数自变量（也就是模型参数）的取值过程，也被简称为损失函数求解。

图形展示损失函数

• 这只能参数维度很低时用，比如就俩参数，画个三维图
• 介绍这个的目的主要是为了介绍函数凹凸性

为了更好的讨论损失函数（SSELoss）求最小值的过程，对于上述二元损失函数来说，我们可以将其展示在三维空间内：三维空间坐标分别为w、b、SSELoss。此处我们可以使用Python中matplotlib包和Axes3D函数进行三维图像绘制 $$ SSELoss(w, b) = (y_1 - ŷ_1)^2 + (y_2 - ŷ_2)^2 = (2 - w - b)^2 + (4 - 3w - b)^2 $$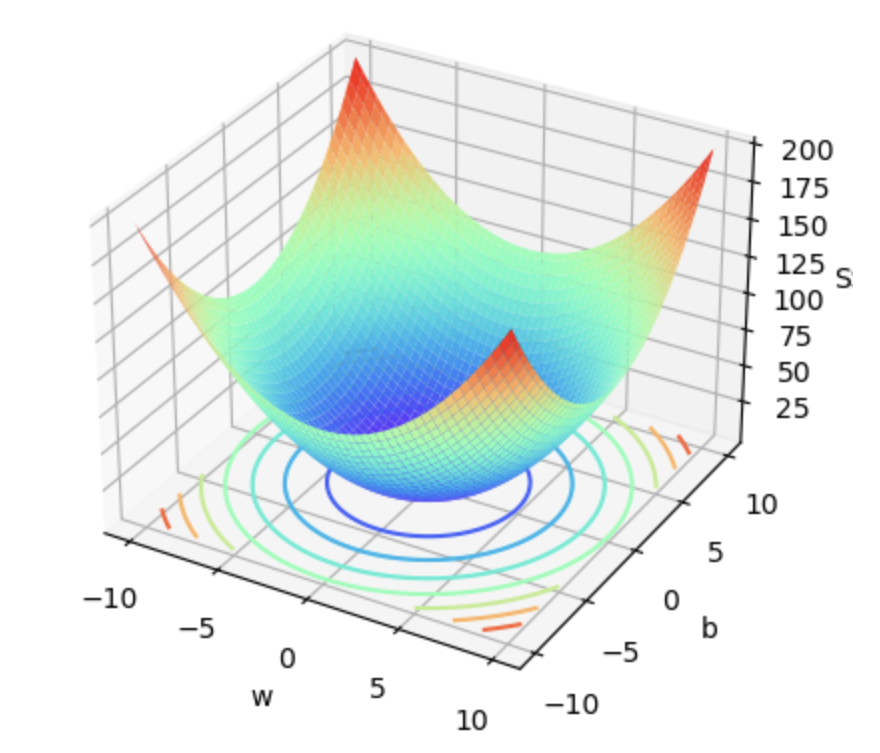

根据图像，我们大概能判断损失函数最小值点位置。画图代码在Practice.ipynb里

这个方法只适用于参数特别少的情况下，才能画的出图，比如就俩参数w，b。但介绍这个方法最主要的目的是想要介绍函数凹凸性，因为在求解损失函数极小值时，损失函数是否为凸函数，非常重要，因为它具有一些有利的性质，使得优化过程更加稳定和可靠。

凸函数定义：对于任意一个函数，如果函数f(x)上存在任意两个点，$x_1, x_2$，且
$$ \frac{f(x_1) + f(x_2)}{2} >= f(\frac{x_1 + x_2}{2}) $$ 我们就判定，这个函数是凸函数。

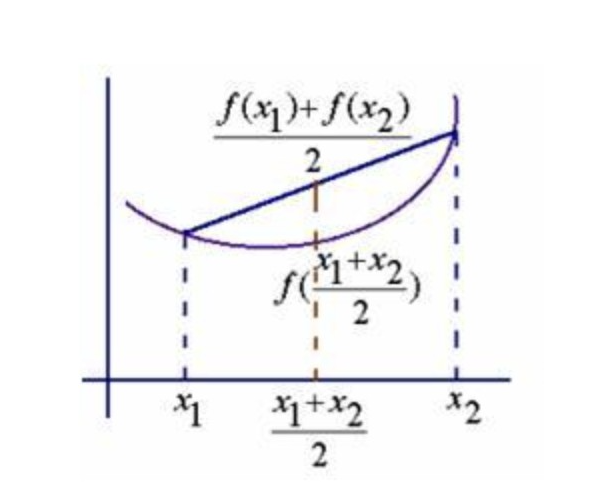
如果损失函数不是凸函数会导致：

1. 陷入局部最优解

   • 多个极值点：非凸函数可能有多个局部最优解（极小值点），这些局部最优解可能不是全局最优解。优化算法在这样的函数上可能会陷入其中一个局部最优解，而无法找到全局最优解。

   • 局部最优解问题：例如，梯度下降法可能会在局部最优解处停下，而不能继续找到其他更好的解。这会导致模型无法达到真正的最优性能。

2. 优化过程不稳定

   • 震荡和收敛缓慢：在非凸函数的优化过程中，优化算法可能会表现出震荡、不稳定或收敛速度缓慢的情况。这是因为非凸函数的形状可能复杂，有很多山峰和洼地。

   • 梯度计算困难：在非凸函数中，梯度可能会在不同区域变化剧烈，导致优化过程的困难和不稳定。并需要更多的计算资源

我们先抛开公式、从一个简单的角度理解最小二乘法。

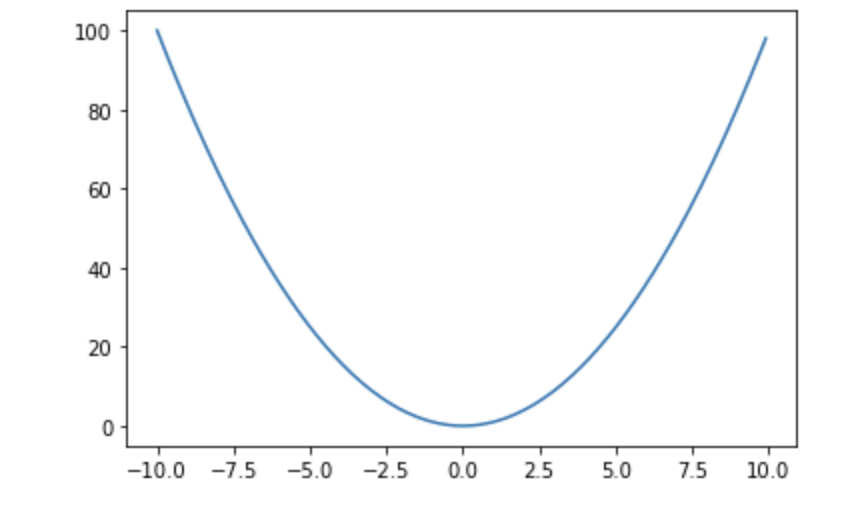
通过上图，也就是$ y = x^2 $函数中不难看出，函数全域最小值点为$x=0$点，同时该点对应的函数切线与x轴平行，也就是在最小值点，函数的导数为0。其实这并不难理解，在最小值点左边函数逐渐递减、而在最小值点右边函数逐渐递增，最小值点左右两边函数单调性相反。

而这种性质其实可以拓展为凸函数的一个关于求解最小值的一般性质，即：

1. 对于一元函数，如果存在导数为0的点，则该点就是最小值点；
2. 对于多元函数，如果存在某一点，使得函数的各个自变量的偏导数都为0，则该点就是最小值点。

据此，我们就找到了最小二乘法求解凸函数最小值的基本出发点：即通过寻找损失函数导函数（或者偏导函数联立的方程组）为0的点，来求解损失函数的最小值。

接下来，尝试利用最小二乘法求解SSELoss。根据上述理论，我们使用最小二乘法求解SSELoss，即 $$ SSELoss= (2 - w - b)^2 + (4 - 3w - b)^2 $$ ，本质上就是在找到能够令损失函数偏导数取值都为零的一组$(w,b)$。SSELoss的两个偏导数计算过程如下： $$ \frac{\partial{SSELoss}}{\partial{(w)}}
& = 2(2-w-b)(-1) + 2(4-3w-b)(-3)\ & = 20w+8b-28 \ & = 0 $$

$$ \frac{\partial{SSELoss}}{\partial{(b)}}
& = 2(2-w-b)(-1) + 2(4-3w-b)(-1)\ & = 8w+4b-12 \ & = 0 $$

最终可得，损失函数最小值点为(1,1)，即当w=1,b=1时模型损失函数计算结果最小、模型SSE取值最小、模型效果最好，此时SSE=0，线性回归模型计算结果为： $$ 𝑦=𝑥+1 $$ 至此，我们就完成了一个机器学习建模的完整流程。

机器学习建模一般流程

Step 1：提出基本模型

• 首先需要明确要解决的问题是什么，如例如分类问题、回归问题、聚类问题等。
• 根据问题的性质选择合适的模型。
• 选择模型参数
  • 例如：
    • 对于线性回归，选择是否使用正则化（L1或L2）。
    • 对于决策树，设置树的深度、最小样本数等。
    • 对于K-means，选择聚类数目（K）。

Step 2：确定评估指标和损失函数

常见的评估指标

常见的评估指标根据问题类型有所不同。以下是各类问题中常见的评估指标：

• 分类问题

  • 准确率 (Accuracy)：正确分类的样本占总样本的比例。
  • 精确率 (Precision)：正确分类的正样本占预测为正样本的比例。
  • 召回率 (Recall)：正确分类的正样本占所有实际正样本的比例。
  • F1 分数 (F1 Score)：精确率和召回率的调和均值。
  • AUC-ROC (Area Under Curve - Receiver Operating Characteristic)：ROC 曲线下的面积，衡量分类模型的性能。
  • 混淆矩阵 (Confusion Matrix)：包含真正例、假正例、真负例和假负例的矩阵。

• 回归问题

  • 均方误差 (MSE - Mean Squared Error)：预测值与真实值之间差值的平方和的平均。
  • 均方根误差 (RMSE - Root Mean Squared Error)：均方误差的平方根，反映预测误差的标准差。
  • 平均绝对误差 (MAE - Mean Absolute Error)：预测值与真实值之间绝对差值的平均。
  • R² 系数 (R-squared)：解释变量所占总变异的比例，衡量模型的拟合优度。

• 聚类问题

  • 轮廓系数 (Silhouette Score)：衡量样本在自身簇内的紧密度与与其他簇的分离度。
  • Calinski-Harabasz 指数 (Calinski-Harabasz Index)：衡量簇内紧密度和簇间分离度的比率。
  • Davies-Bouldin 指数 (Davies-Bouldin Index)：衡量簇内相似度和簇间差异的比率，值越小表示聚类效果越好。
  • SSE (Sum of Squared Errors)：样本点到其簇中心的平方差和。

• 排序问题

  • NDCG (Normalized Discounted Cumulative Gain)：基于排序结果的相关性度量，用于评估推荐系统的效果。
  • MAP (Mean Average Precision)：平均精度，用于评估信息检索系统的排序性能。

• 异常检测

  • F1 分数 (F1 Score)：在异常检测中，精确率和召回率的调和均值。
  • AUC-ROC (Area Under Curve - Receiver Operating Characteristic)：ROC 曲线下的面积，用于衡量异常检测模型的性能。

常见损失函数

• 分类问题

  • 对数损失（Log Loss）/交叉熵损失（Cross-Entropy Loss）

  • Hinge 损失（Hinge Loss）

  • 多类交叉熵损失（Categorical Cross-Entropy）

  • Kullback-Leibler 散度（KL Divergence）

• 回归问题

  • 均方误差（MSE）

  • 平均绝对误差（MAE）

  • Huber 损失（Huber Loss）

• 聚类问题

  • 平方误差（SSE）

  • 轮廓系数（Silhouette Score

• 排序问题

• 排序损失（Rank Loss）

• NDCG（Normalized Discounted Cumulative Gain）

• 异常检测

  • 孤立森林损失（Isolation Forest Loss）

Step 3：根据损失函数性质，选择优化方法

判断损失函数凹凸性，根据凹凸性选择不同的优化方法

根据凹凸性选择优化方法

1. 凸函数：

   • 最小二乘法 (Least Squares Method)：专门用于线性回归中的凸优化问题，通过最小化平方误差来拟合模型。

   • 梯度下降 (Gradient Descent)：适用于求解凸函数的最小值，通常收敛较好。

   • 牛顿法 (Newton's Method)：利用二阶导数加速收敛，适用于凸函数，但计算成本较高。

   • 拟牛顿法 (Quasi-Newton Methods)：如BFGS，适用于中等规模的凸优化问题。

   • 共轭梯度法 (Conjugate Gradient Method)：适合求解大型稀疏线性系统和优化问题。

2. 非凸函数：

   • 随机梯度下降 (SGD - Stochastic Gradient Descent)：适用于大型数据集的非凸优化问题，能帮助跳出局部最优。
   • 模拟退火 (Simulated Annealing)：一种全局优化方法，可以探索整个搜索空间，适合处理具有多个局部最优的非凸函数。
   • 遗传算法 (Genetic Algorithms)：通过模拟自然选择过程，适用于复杂的非凸优化问题。
   • 变分优化 (Variational Optimization)：用于处理复杂模型中的非凸损失函数，如变分自编码器中的优化。

Step 4.利用优化算法进行损失函数求解

求损失函数极小值及其对应的参数