什么是交叉相关分析（）？

交叉相关是一种用于衡量两个时间序列之间相似程度的统计方法。通过计算一个序列与另一个序列在不同时间滞后（或超前）情况下的相关性，可以发现它们之间的关系或模式。例如，在时间序列分析中，可以用交叉相关来判断两个变量之间是否存在某种时间上的依赖关系。

交叉相关分析的公式

交叉相关的计算公式为： $$ R_{xy}(k) = \frac{1}{N-k} \sum_{t=1}^{N-k} (x_t - \bar{x})(y_{t+k} - \bar{y}) $$ 其中：

$R_{xy}(k)$是滞后 kkk 时的交叉相关系数。
$x_t$和 $y_t$ 是两个时间序列的数据点。
$\bar{x}$和 $\bar{y}$分别是序列 $x$ 和 $y$ 的均值。
$N$是时间序列的长度。

使用交叉相关分析的场景

经济分析：衡量不同经济指标之间的时间关系。
信号处理：分析两个信号的相关性。
市场营销：评估促销活动与销售数据之间的时滞效应。
- 举个栗子：
  Suntory的一个实验：在便利店发放优惠券，内容是免费领取一瓶新品酒，假设顾客在便利店免费体验后，认为商品好，之后会在超市购买该商品。
  具体分析过程如下：
  1. 初步假设与构成比分析：先分析各商品在便利店和超市的销量构成比，假设：超市的销量构成比会随着便利店的销量构成比变化，即顾客通过优惠券体验后，应该会去超市购买该商品。
    结果发现，超市的销量构成比并未随着便利店的销量构成比发生变化。
  2. 探索时间滞后效应：因此，可能是由于时间滞后效应，即超市的销量构成比虽然应该会受到便利店销量变化的影响，但反应较慢，可能会在几周后才显现出来。基于此，进一步进行了交叉相关性分析。
    结果发现，在第0周时，两者的关联性最强，未发现明显的时间滞后效应。因此，可以得出结论：发放优惠券并不会促进顾客在超市的购买，顾客主要是利用优惠券免费获得商品，并没有继续在超市购买。

上述案例示例代码

数据我造的

python

import numpy as np
import matplotlib.pyplot as plt
import warnings

# 设置中文字体
warnings.filterwarnings('ignore')
plt.rcParams['font.family'] = 'Hiragino Sans GB'
plt.rcParams['axes.unicode_minus'] = False 

# 示例数据：便利店（CVS）和超市（SM）的销量数据
cvs_sales = np.array([100, 150, 200, 250, 300])  # 便利店销量
sm_sales = np.array([99, 98, 99, 100, 102])  # 超市销量

# 绘制时间序列图
plt.figure(figsize=(10, 6))
plt.plot(cvs_sales, label='便利店销量', marker='o')
plt.plot(sm_sales, label='超市销量', marker='s')
plt.title('便利店与超市销售时间序列')
plt.xlabel('时间（周）')
plt.ylabel('销售数量')
plt.legend()
plt.grid(True)
plt.show()



# 计算交叉相关
cross_corr = np.correlate(cvs_sales - np.mean(cvs_sales), sm_sales - np.mean(sm_sales), mode='full')

# 计算滞后值（周）
lags = np.arange(-len(cvs_sales) + 1, len(cvs_sales))

# 找到最大相关性及其滞后值
max_corr = np.max(cross_corr)
best_lag = lags[np.argmax(cross_corr)]

# 输出结果
print(f'最大交叉相关值: {max_corr}')
print(f'最佳滞后值: {best_lag} 周')

# 绘制交叉相关图
plt.figure(figsize=(10, 6))
plt.plot(lags, cross_corr, marker='o')
plt.title('便利店与超市销量的交叉相关')
plt.xlabel('滞后值（周）')
plt.ylabel('交叉相关值')
plt.grid(True)
plt.show()

# 结论分析
if best_lag == 0:
    print("结果：未发现明显的时间滞后效应，便利店的优惠券发放未促进超市销量的增加。")
else:
    print(f"结果：在滞后{best_lag}周时，超市销量对便利店销量产生了响应。")

代码解释：

数据准备：cvs_sales 和 sm_sales 分别表示便利店和超市的销售数据。
计算交叉相关：使用np.correlate函数计算两个序列的交叉相关。
滞后计算：使用lags数组表示不同的时间滞后值。
结果分析：打印最大交叉相关值及最佳滞后值，表明在最佳滞后情况下两个序列的相关性最强。
可视化：
- 时间序列图，看超市销量有没有跟随便利店变化
- 交叉相关图，看超市销量没有追随便利店变化是不是因为时间滞后效应

上述可视化的图

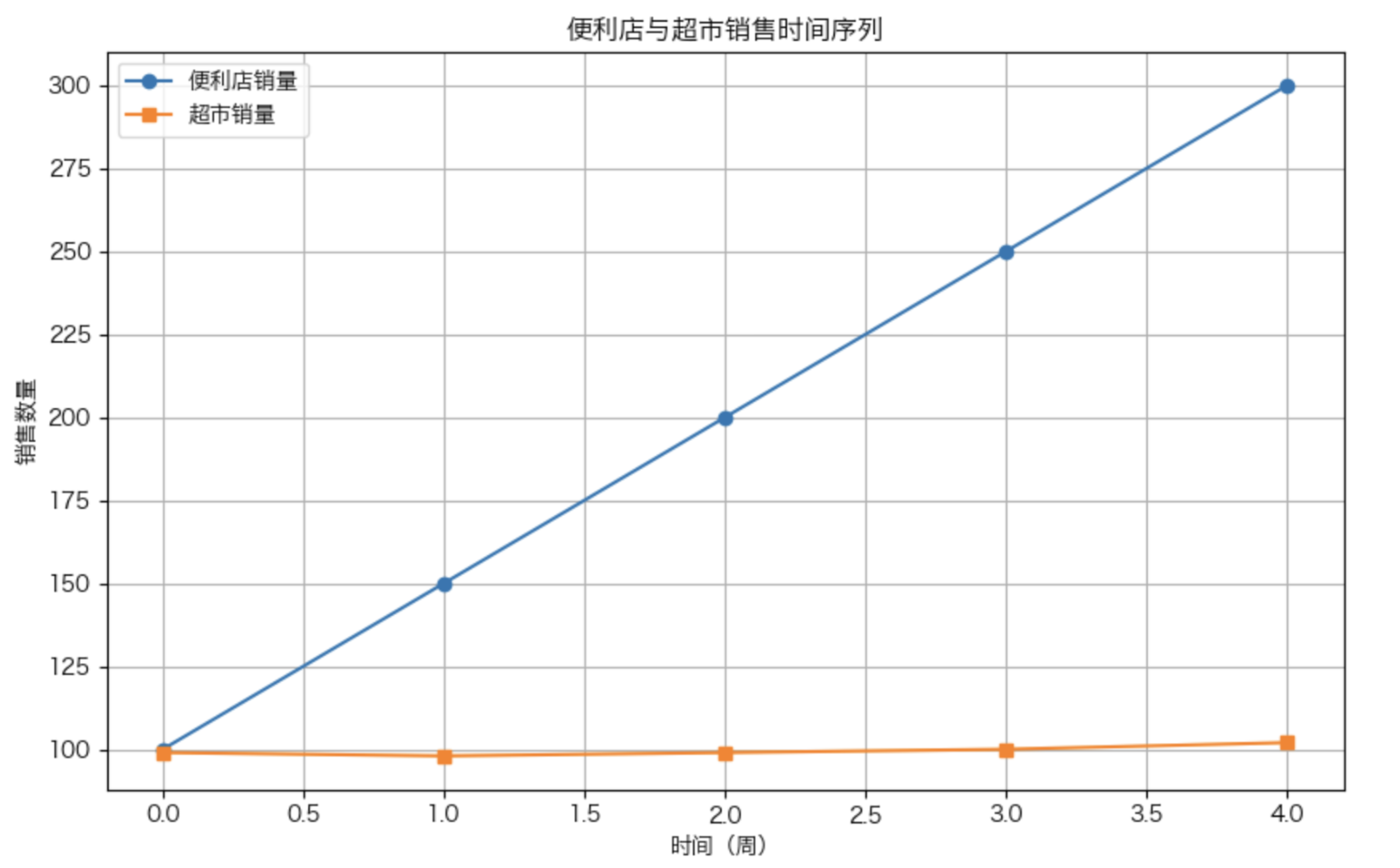
从上图可以看出超市销量并未追随便利店的变化，因此考虑超市销量没有追随便利店变化是不是因为时间滞后效应，画下图

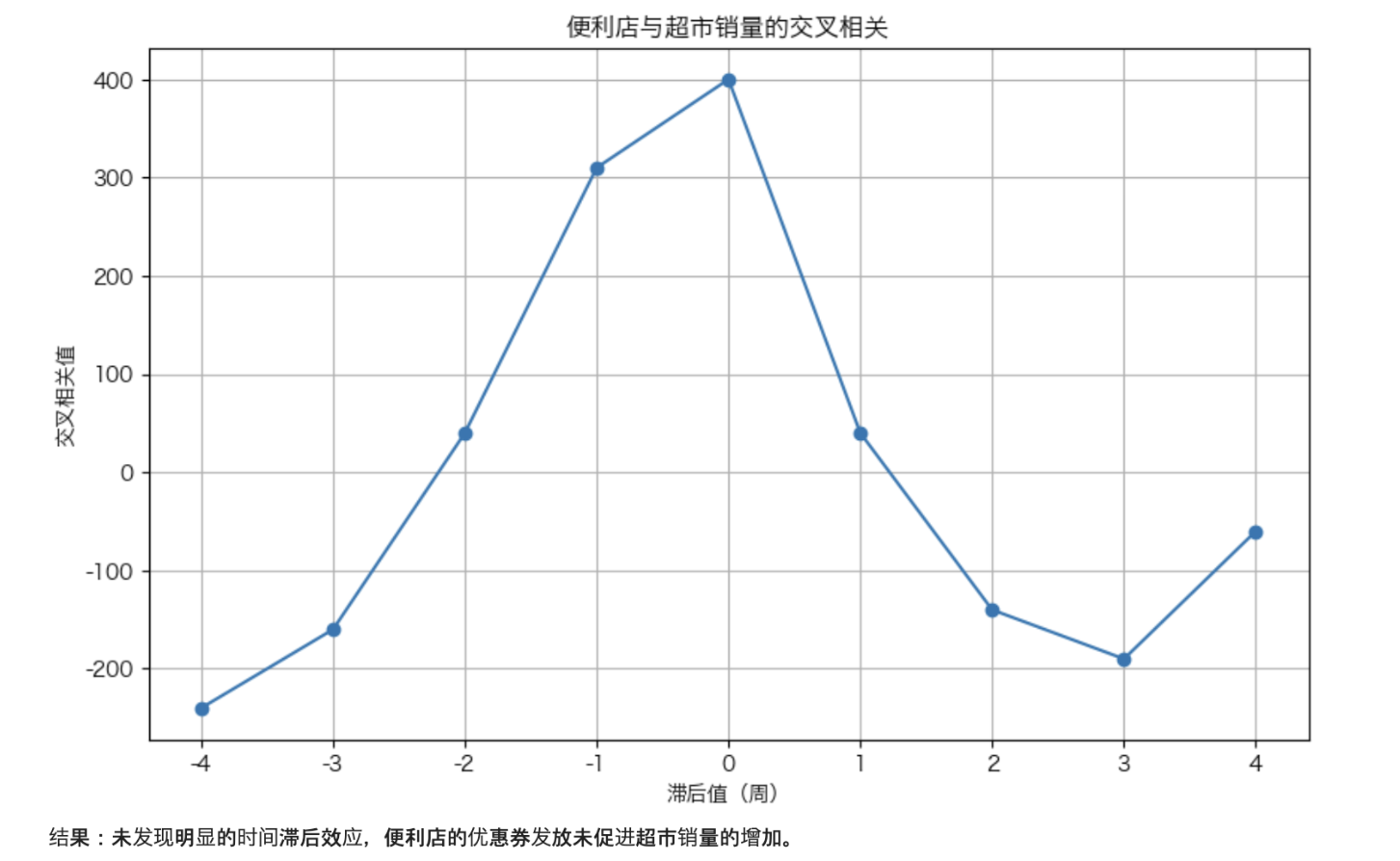
总结

交叉相关是一种强大的工具，可以用来分析两个时间序列之间的关系，特别是在寻找时间上的滞后效应或同步性时。通过计算不同滞后情况下的相关性，可以识别潜在的模式或依赖关系，从而为决策提供支持。

什么是交叉相关分析（）？ ​

交叉相关分析的公式 ​

使用交叉相关分析的场景 ​

上述案例示例代码 ​

代码解释： ​

上述可视化的图 ​