差分的差分 DID（DIfference of Difference）

主要是为了考虑时间推移的影响
先假设对照组和实验组
其中对照组按时间，去两组数据y_control_1，y_control_2
实验组同样按照时间，y_treat_1，y_treat_2
y_treat_2 减去 y_treat_1 得到的结果，同时混杂着时间因素和政策因素。

假设前提

假设前提：DID有一个很重要且很严格的平行趋势假设，即实验组和对照组在没有干预的情况下，结果的趋势是一样的。

代码

https://cloud.tencent.com/developer/article/2325287 腾讯的

准备数据

python


from faker import Faker
from faker.providers import BaseProvider, internet  # faker是用来创造虚拟数据的库
from random import randint
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import math
import statsmodels.formula.api as smf
import warnings

warnings.filterwarnings('ignore')

# 绘图初始化
%matplotlib inline
sns.set(style="ticks")

python

# 自定义数据
fake = Faker('zh_CN')
class MyProvider(BaseProvider):
    def myCityLevel(self):
      #随机返回一个城市类别
        cl = ["一线", "二线", "三线", "四线+"]
        return cl[randint(0, len(cl) - 1)]
    def myGender(self):
      # 随机返回一个性别
        g = ['F', 'M']
        return g[randint(0, len(g) - 1)]
fake.add_provider(MyProvider)

# 构造假数据，模拟用户特征
uid=[]
cityLevel=[]
gender=[]
for i in range(10000):
    uid.append(i+1)
    cityLevel.append(fake.myCityLevel())
    gender.append(fake.myGender())
    
raw_data= pd.DataFrame({'uid':uid,
                        'cityLevel':cityLevel,
                        'gender':gender,
                       })

raw_data['class'] = raw_data['uid'].map(lambda x: 'A' if x % 2 == 1 else 'B') # 按奇偶随机分组

# 构造did数据
df = pd.DataFrame(columns=['uid','cityLevel','gender', 'class', 'sales', 'dt'])
for i,j in enumerate(range(2005,2011)):
    lift = 1+i*0.05   #为了做一个偏差，
    df_temp = raw_data.copy()
    
    #np.random.normal()里面穿三个参数，平均值，方差，样本量size
    df_temp['sales'] = [int(x) for x in np.random.normal(300*lift, 60*lift, df_temp.shape[0])]
    
    # 假设因为政策冲击A组（实验组）销量将为88%
    df_temp['sales'] = df_temp.apply(lambda x: x.sales*0.88 if x['class']=='A' else x.sales, axis=1)
    
    #2007年之后，时间因素的影响对照组B的销量导致增加0.02
    if j>2007:
        df_temp['sales'] = df_temp.apply(lambda x: x.sales*(1+i*0.02) if x['class']=='B' else x.sales, axis=1)
    df_temp['dt'] = j
    df=pd.concat([df,df_temp])
    
df_did = df.groupby(['class', 'dt'])['sales'].sum().reset_index()

验证平行趋势假设

python

# 计算文字的y坐标
y_text = df_did.query('dt == 2007 and `class`=="B"')['sales'].values[0]
# 绘图查看干预前趋势
fig, ax = plt.subplots(figsize=(12,8))
sns.lineplot(x="dt", y="sales", hue="class", data=df_did)
ax.axvline(2007, color='r', linestyle="--", alpha=0.8)   # axvline函数表示画纵向虚线
plt.text(2007, y_text, 'treatment')
plt.show()

除了画图观察平行趋势，也可以通过回归拟合，参考自https://www.yisu.com/jc/614478.html

python

# 方法2 回归计算
df_did['t'] = df_did['treatment'].map(lambda x: 1 if x=='干预后' else 0) # 是否干预后
df_did['g'] = df_did['class'].map(lambda x: 1 if x=='B' else 0) # 是否试验组
df_did['tg'] = df_did['t']*df_did['g'] # 交互项

# 回归
est = smf.ols(formula='sales ~ t + g + tg', data=df_did).fit() 
print(est.summary())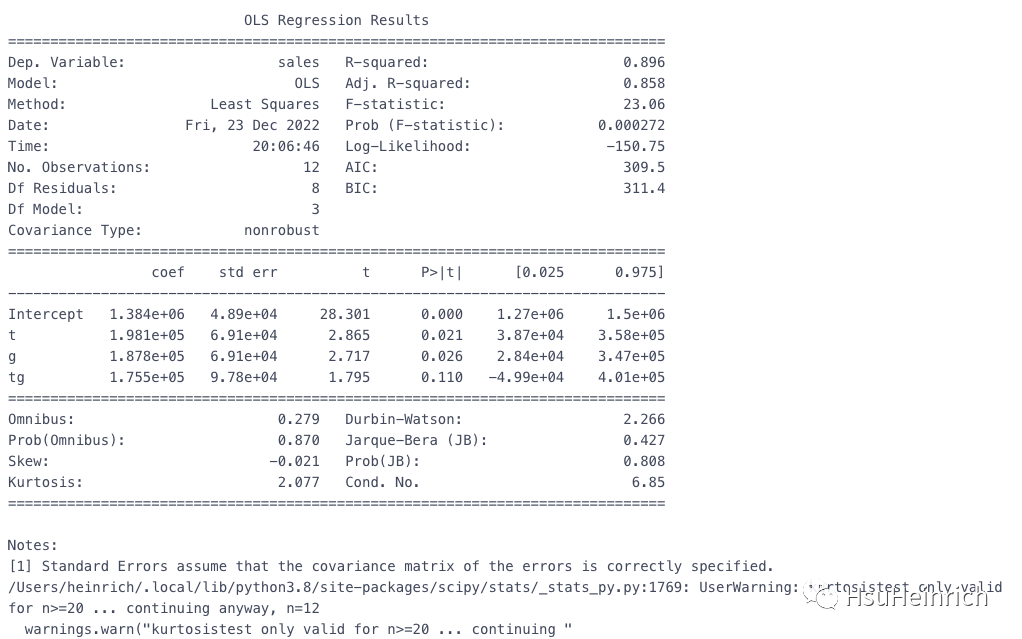

tg的P是0.110，大于0.05，效果不显著，也就是说具备平行趋势，政策没有产生影响。

python

# 计算因果效应
df_did['treatment'] = df_did['dt'].map(lambda x: '干预后' if x>2007 else '干预前')
df_did_cal = df_did.groupby(['class', 'treatment'])['sales'].mean()
did = (df_did_cal.loc['B', '干预后'] - df_did_cal.loc['B', '干预前']) - \
        (df_did_cal.loc['A', '干预后'] - df_did_cal.loc['A', '干预前'])
print(did)

差分的差分 DID（DIfference of Difference） ​

假设前提 ​

代码 ​

差分的差分 DID（DIfference of Difference）

假设前提

代码