极大似然估计(MLE)
【【机器学习】重新理解线性回归 - 1 - 极大似然估计】 https://www.bilibili.com/video/BV1QM4y167oZ/?share_source=copy_web&vd_source=51cc2cdad73ec82b95881f9d39cacb48
基本思想
极大似然估计(Maximum Likelihood Estimation, MLE)是一种用于估计统计模型参数的方法。比如求解线性回归模型`y=wx+b的最优参数,w和b。它的基本思想是找到一组参数,使得在这些参数下,观测数据出现的概率最大。
以线性回归模型为例,在经典的线性回归模型中,假设误差项(残差)服从高斯分布。
高斯分布的概率密度函数如下: $$ f(x) = \frac{1}{\sqrt{2\pi\sigma^2}} \exp\left(-\frac{(x - \mu)^2}{2\sigma^2}\right) $$ 这个概率密度函数看着虽然复杂,但核心就俩参数$\mu$和$\sigma$
数据集中某特征的数据,服从高斯分布(经典线性回归模型的假设),从该特征中采样,采样而来的每一个数据互不影响,而且是从同一个分布中获得的。因此这样的采样结果可以称为独立同分布。独立同分布是大部分算法模型的重要假设。
问题来了,如何从这些独立同分布的采样数据逆推出高斯分布的参数,$\mu$和$\sigma$?
高斯分布的定义域是负无穷到正无穷,因此从理论上来说,无论$\mu$和$\sigma$等于多少,都有可能采样出上面的数据,区别只是概率大小,因此我们想知道的是,$\mu$和$\sigma$等于多少时,能让采样数据出现的概率最大,此时的$\mu$和$\sigma$就是我们要求的高斯分布的参数。
下图的每一个样本点被采样的概率都可以写成一个条件概率的形式,又因为这些数据点满足独立同分布,因此他们的联合概率就是各个条件概率的连乘。然后求使得这个联合概率最大的$\mu$和$\sigma$就是我们要求的高斯分布的参数。这就是极大似然估计的基本思想。

极大似然估计是如何求解模型参数的
由于概率是[0,1]的数值,大量连乘后,会导致似然值无限趋近于0,使得求参数变难,因此通过$ln$将连乘转换为连加。

现在回头重看线性回归:
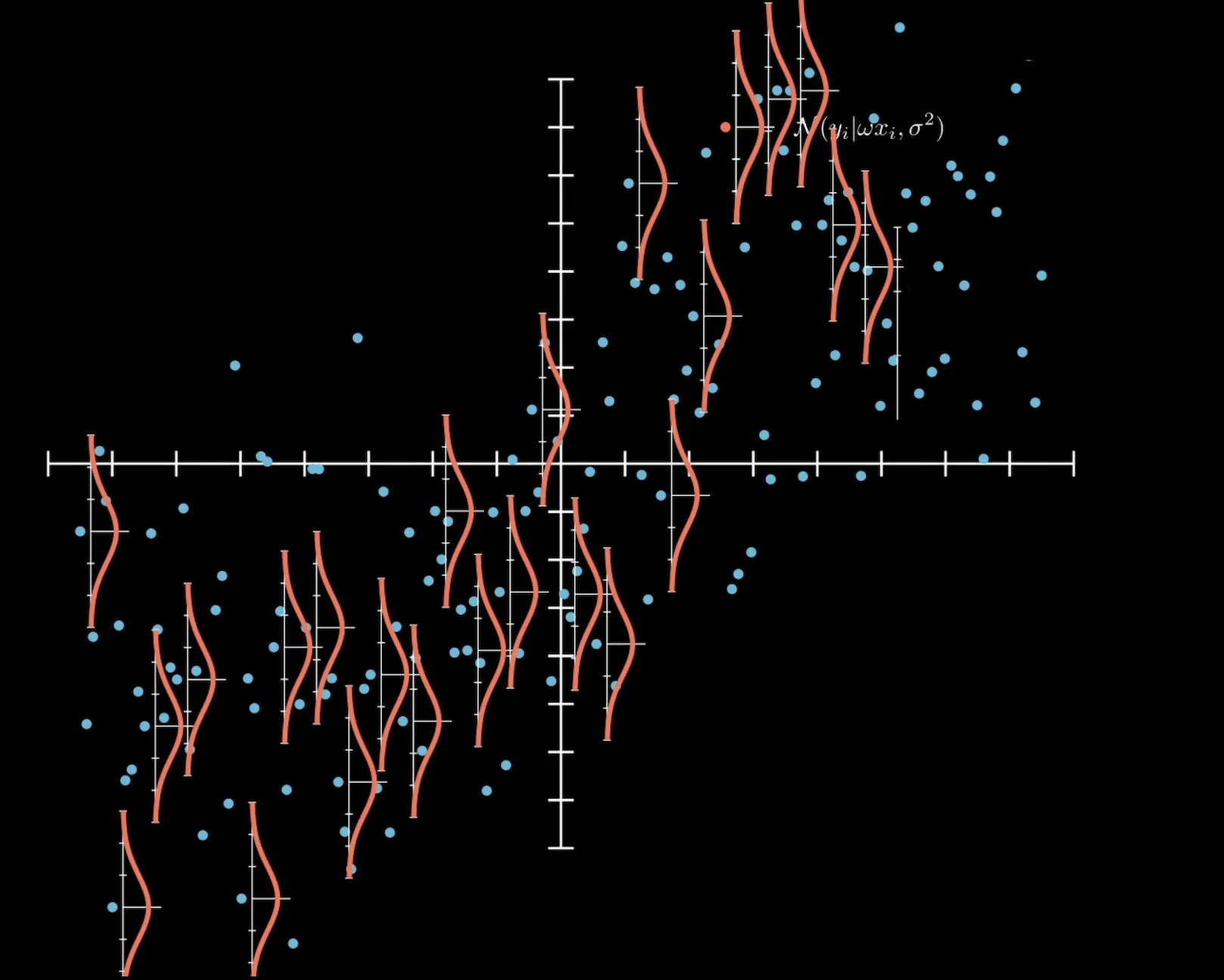
之前是将数据看成一组组x和y的对应,现在将x和y分开看待。将目标值Y看作是从一个高斯分布中采样而来的数据,在给定X的情况下,y是不确定的,现在的y不过是其中一种可能的采样结果。如下图所示
根据线性回归$y=wx+b$的方程,又因为b可以看作是$w0$,因此$y=wx$,又因为y服从均值为0,方差为$\sigma^2$的高斯分布,相当于给$y$增加了一个均值为0的噪声项,即$y_i = wx_i + \epsilon_i$,其中$\epsilon \sim \mathcal{N}(0, \sigma^2)$
因此$y_i \sim \mathcal{N}(w x_i, \epsilon_i)$
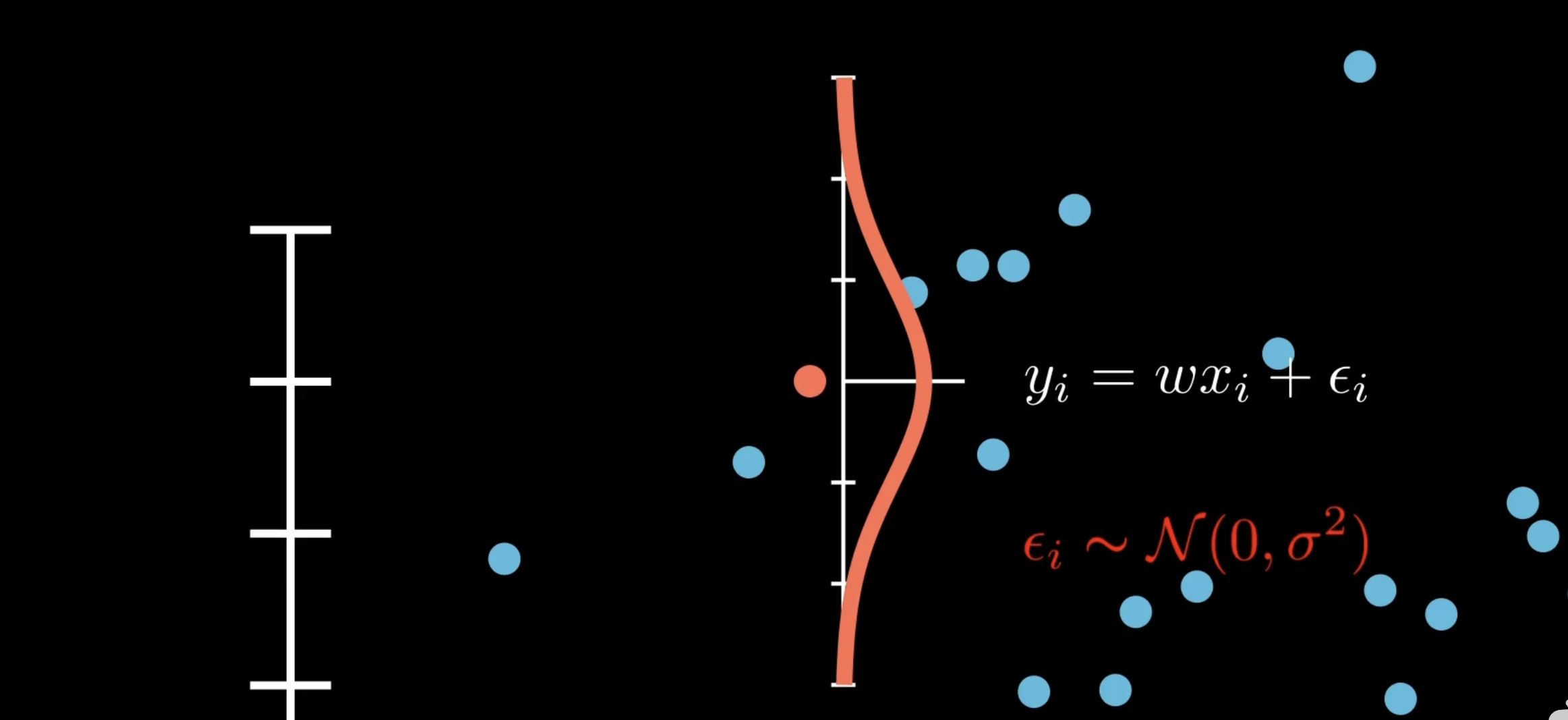
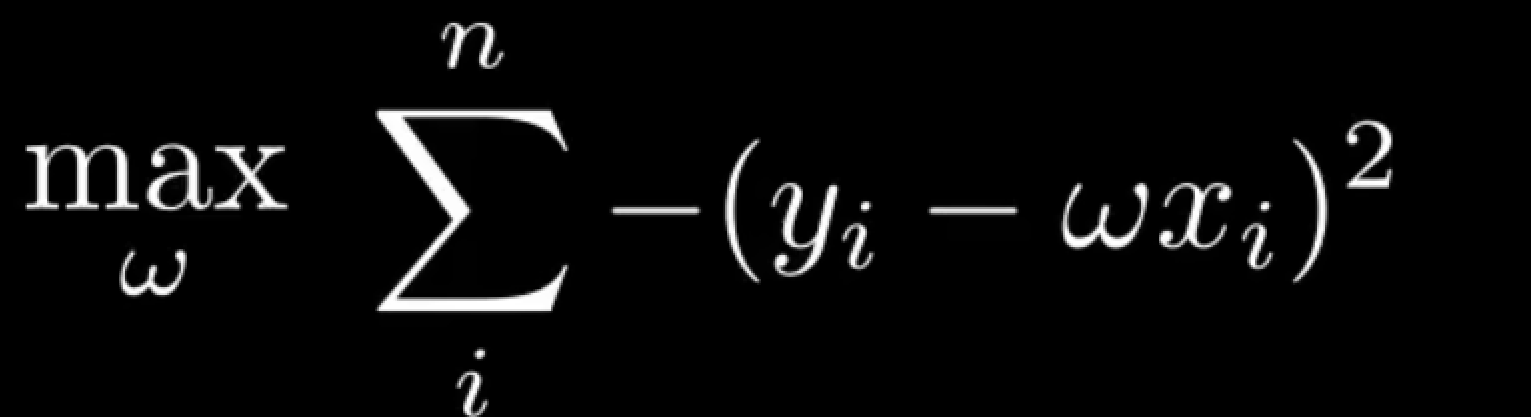
这种依赖于条件分布的假设在机器学习中叫做判别式模型,假设所有数据都遵循同一个条件分布,且数据点相互独立,那么就可以进行极大似然估计。
将$y_i \sim \mathcal{N}(w x_i, \epsilon_i)$带入高斯分布的概率密度函数,得到似然函数
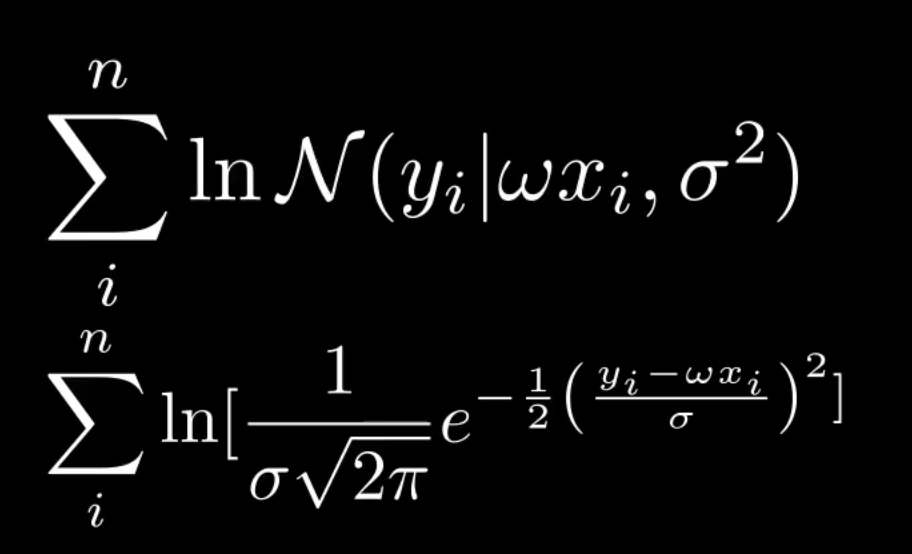
化简后:
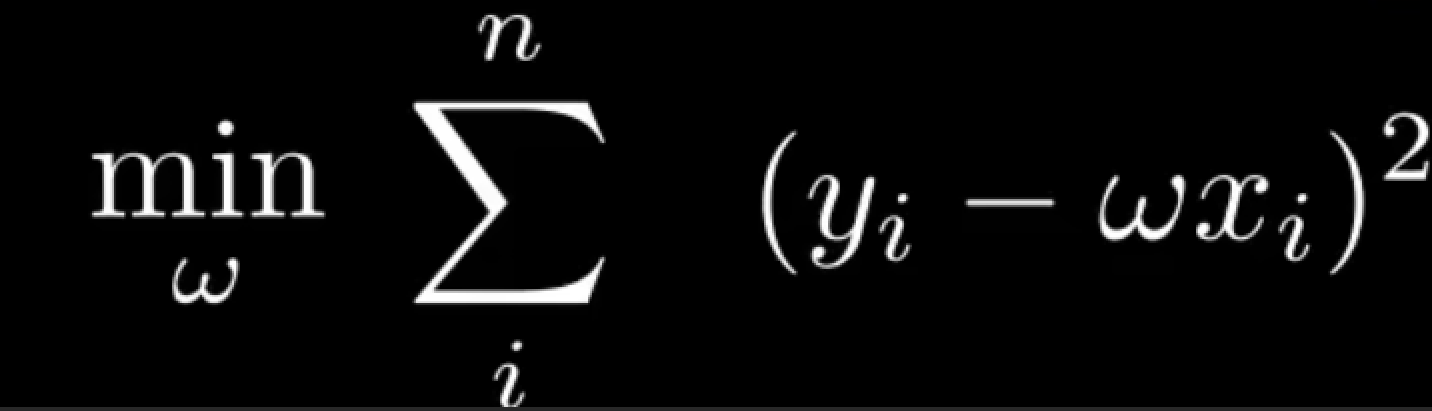
由于$\sigma$是模型噪声,与参数无关,因此可以从上式中剔除。
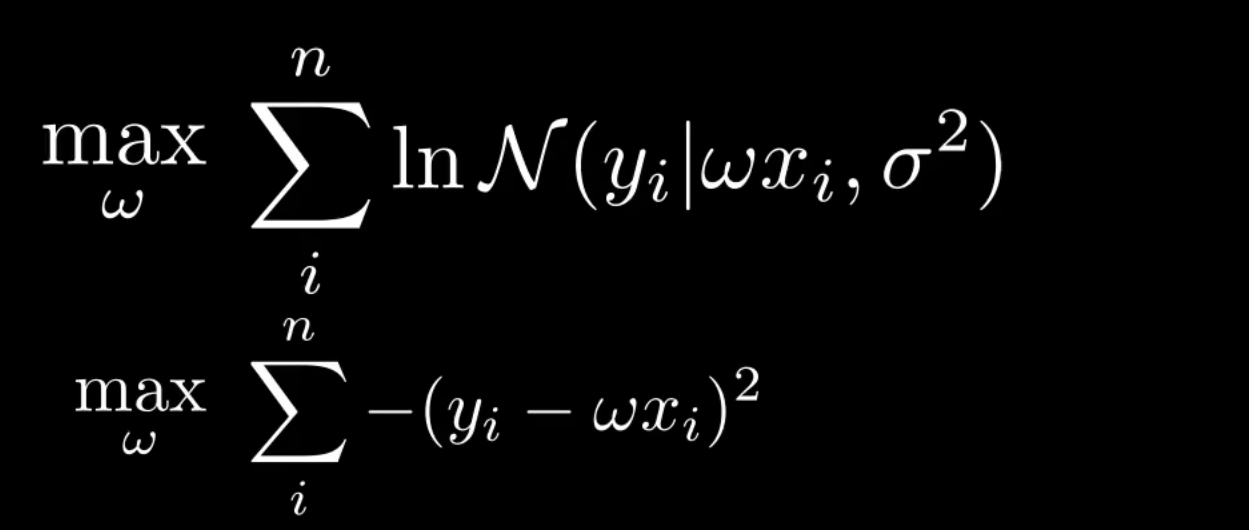
求最大值,等于求最小值的负值,因此
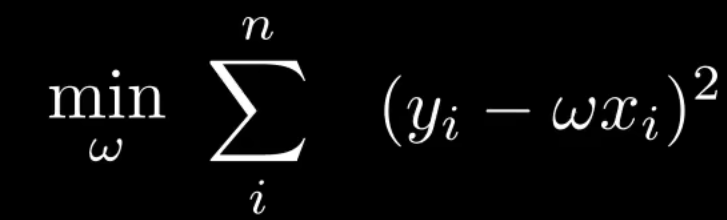
于是,又重新得到了最小二乘法。因此最小二乘法,是极大似然估计在高斯分布下的一种特殊形式。
其他分布下的极大似然估计
【【机器学习】重新理解线性回归 - 2 - 广义线性模型:sigmoid函数到底是怎么来的】 https://www.bilibili.com/video/BV13X4y1R7im/?share_source=copy_web&vd_source=51cc2cdad73ec82b95881f9d39cacb48
【【机器学习】重新理解线性回归 -3- 交叉熵】 https://www.bilibili.com/video/BV1HL411B7hh/?share_source=copy_web&vd_source=51cc2cdad73ec82b95881f9d39cacb48
贝叶斯定理
【【官方双语】贝叶斯定理,使概率论直觉化】https://www.bilibili.com/video/BV1R7411a76r?vd_source=51cc2cdad73ec82b95881f9d39cacb48
这公式在说什么
$$ \begin{equation} P(A|B) = \frac{P(B|A) \cdot P(A)}{P(B)} \end{equation} $$ 举个例子,steven是一个注重细节,温文尔雅的人,你觉得他是一个农民还是一个图书管理员?
大部分人会回答图书管理员,但是他们忽略了现实生活中农民和图书管理员的比例,在美国这个数字是20:1。
假设现在有200个农民,10个图书管理员,假设在图书管理员中注重细节,温文尔雅的比利是40%,农民中注重细节,温文尔雅的比例是10%,那么现在就有4个图书管理员,和20个农民具备注重细节,温文尔雅的特征。

所以现在从这24个人中随机抽取一个,他是图书管理员的概率为16.7%。
所以即使你认为图书管理员注重细节,温文尔雅的可能性远高于农民,但是架不住农民数量多啊,上面的直觉从统计学的角度是错的
所以贝叶斯定理,也就是这个公式真正的根本性结论是:新的证据不能直接凭空决定你的结论,而是要更新先验概率(比如农民和图书管理员在现实生活中的比例20:1)
定义一些数学概念
在上述例子中,
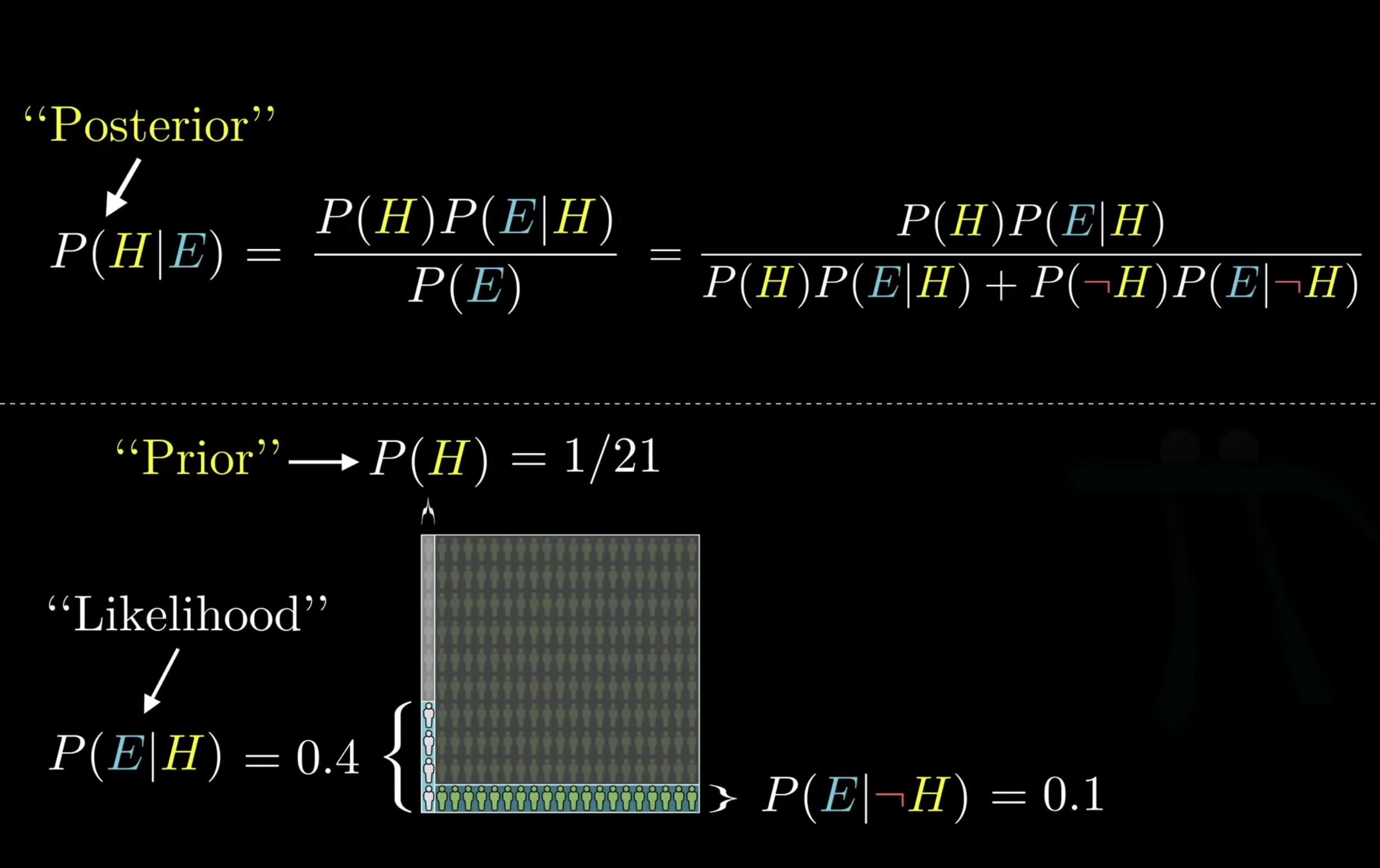
- 先验概率(prior):图书管理员和农民的比例为1:20,所以图书管理员的概率$P(H)=1/21$ 为先验概率
- 似然概率(likelihood):图书管理员温文尔雅的概率为0.4,$P(E|H) = 0.4$
- 后验概率:最终得到的,具有温文尔雅特征且为图书管理员的概率为后验概率