Hong's External Brain

Appearance

各种分布和检验 ​

正态分布 ​

  • 正态分布对应的检验方法是Z检验

  • 主要有两种类型

    • 单样本Z检验（One-sample Z-test）： 用于比较样本均值与已知总体均值。

      • 例如，检验某组学生的平均成绩是否显著高于已知的全国平均成绩。

      • 公式如下：

      • 其中，x̄ 是样本均值，μ 是总体均值，σ 是总体标准差，n 是样本量。

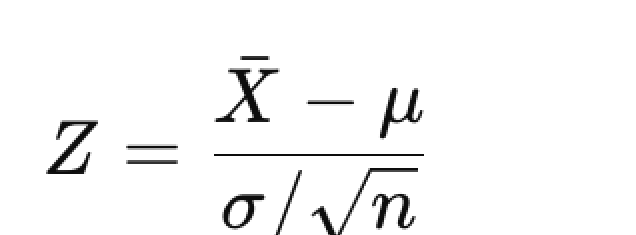
        image-20241221210457603

    • 两样本Z检验（Two-sample Z-test）： 用于比较两个独立样本的均值是否有显著差异。

      • 例如，检验两个不同教学方法下的学生平均成绩是否有显著差异。

      • 公式如下，

      • 其中，x1 bar 和 x2 bar 是两个样本的均值**，σ1** 和 σ2 是两个样本的标准差，n1 和 n2 是样本量。

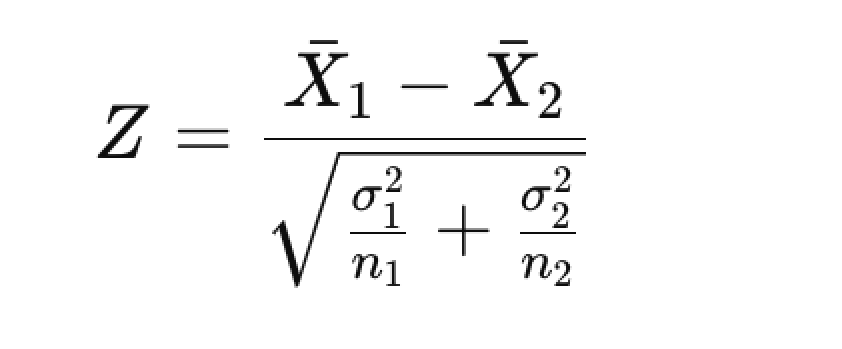
        image-20241221210918014

T检验 ​

【【统计科普】五分钟轻松掌握三大 t 检验 - 独立样本t检验、配对样本t检验与单样本t检验】 https://www.bilibili.com/video/BV1eg411a7eh/?share_source=copy_web&vd_source=51cc2cdad73ec82b95881f9d39cacb48

先举个例子，a班平均成绩80，b班平均成绩82，这样直接比较平均值后就说b班成绩好于a班的说法是没有说服力的，因为存在偶然性。

，t检验相比于直接比较两组数据之间的平均数更有说服力，更具有说服力的理由如下：

现在提出假设：

H0：a班和b班的成绩是相等的

H1：a班和b班的成绩是不相等的

只要证明H0假设成立的可能性低于5%，则拒绝原假设，相较于直接比较平均数更具有说服力

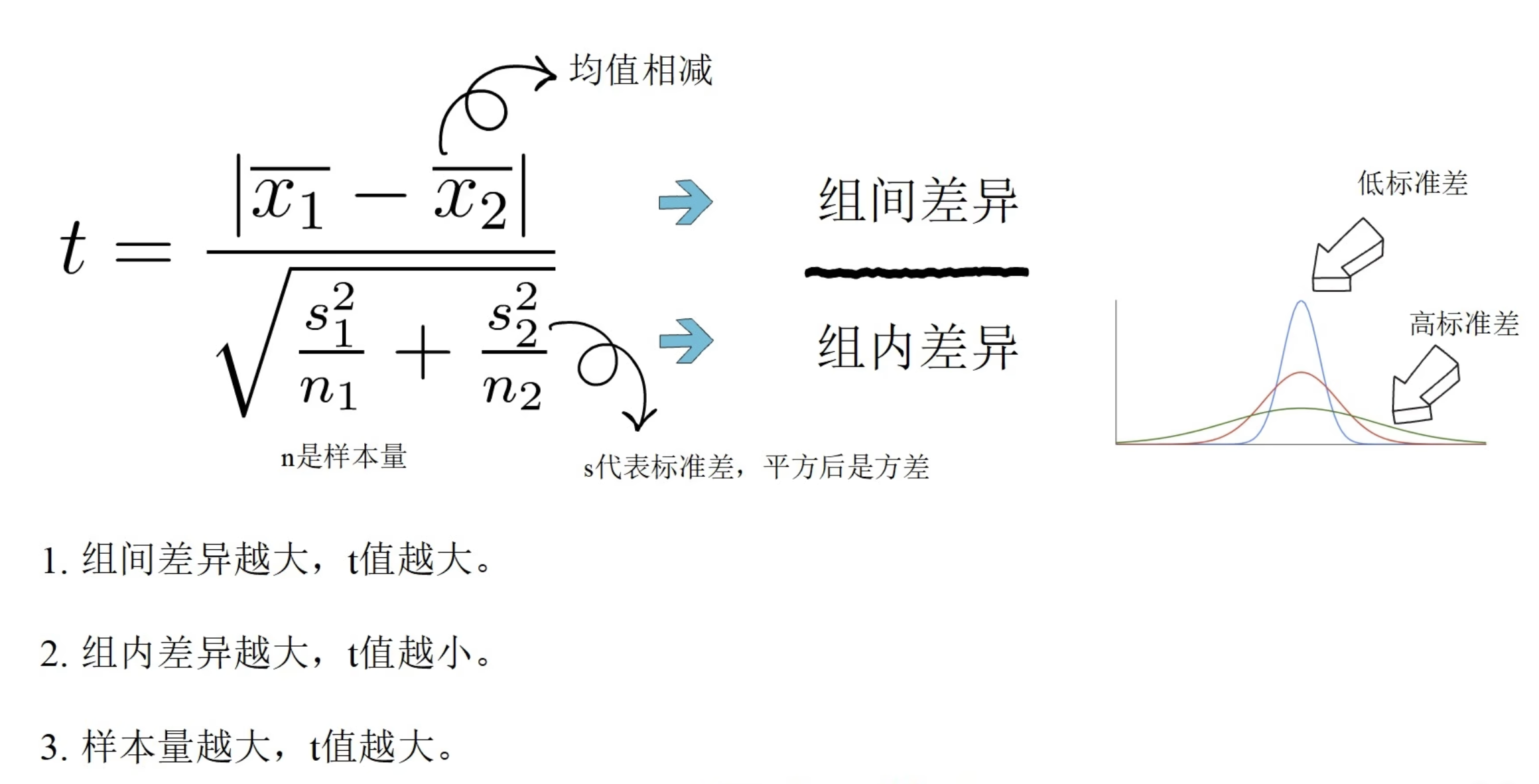
image-20240907194508672

计算出的t值如果大于t临界值，则拒绝原假设，证明a班和b班的成绩是不相等的，又因为a班平均成绩80，b班平均成绩82，因此b班成绩好于a班。

F检验和方差分析（ANOVA） ​

，之前的T检验只能检验两组数据之间均值是否存在显著差异。

先举个例子，现在想看医学，心理学，生物学的学生在推理能力上是否存在显著差异。

医学生平均分，81，心理学学生平均分83，生物学学生平均分87。

这样直接比较平均分，就说生物学学生推理能力更强是没有说服力的，因为存在偶然性。

方差分析相比于，直接比较三组数据之间的平均数更有说服力，更具有说服力的理由如下：

现在提出假设：

H0：医学，心理学，生物学的学生在推理能力是相等的

H1：至少存在一组的均数与其他组不想等。

只要证明H0假设成立的可能性低于5%，则拒绝原假设，相较于直接比较平均数更具有说服力 $$ F = \frac{\frac{1}{k - 1} \sum_{i=1}^{k} n_i (\bar{X}i - \bar{X})^2}{\frac{1}{N - k} \sum^{k} \sum_{j=1}^{n_i} (X_{ij} - \bar{X}_i)^2} $$ 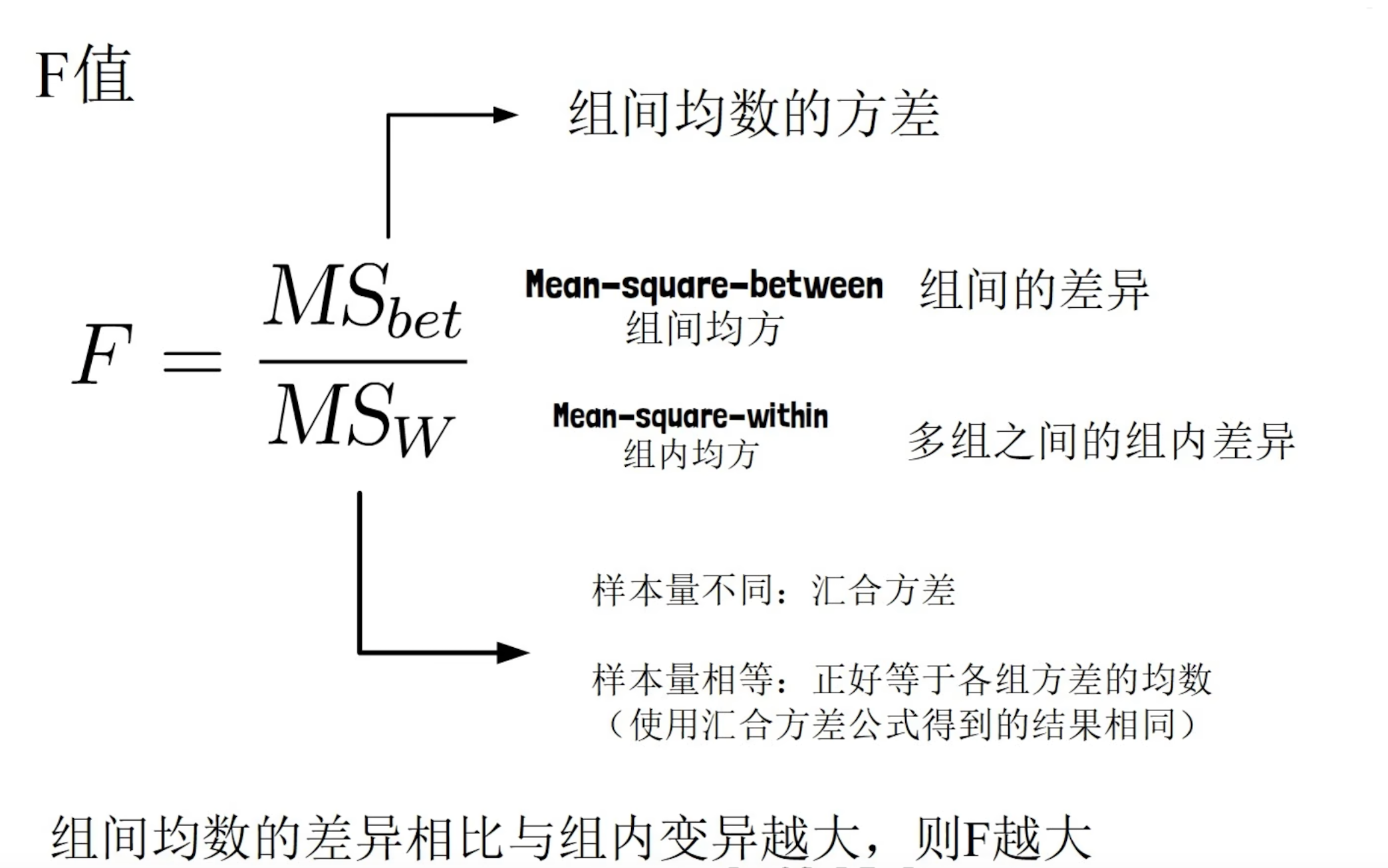image-20241221211237871

同样，计算出的F值如果大于F临界值，则拒绝原假设。

卡方检验 ​

$$ \chi^2 = \sum \frac{(O_i - E_i)^2}{E_i} $$

主要有两种常见的卡方检验：

  • 独立性检验 (Chi-square test of independence)：用于判断两个分类变量是否具有统计上的独立性，即是否存在关联关系。

      • 卡方检验用于衡量每个特征与目标变量之间的关联性。通过检验每个特征与目标变量是否存在显著关联，能够筛选出对目标变量有较强影响的特征。
      • 如果某个特征与目标变量之间的卡方统计量较大，说明该特征和目标变量之间的关联性较强，可以保留该特征。
      • 如果某个特征与目标变量之间的卡方统计量较小，说明它与目标变量的关联性较弱，可以考虑剔除该特征。

  • 拟合优度检验 (Chi-square goodness-of-fit test)：用于判断观测值是否与期望值相符。比如，可以检验一组数据是否符合某种分布。

    • 卡方值越大，说明观测数据和期望数据之间的差距越大，即拟合程度不好。这可能表明数据不符合期望的分布模型，或者模型不适合描述数据。
    • 我们通常根据卡方值对应的p值来做判断。卡方值越大，p值越小。如果 p值小于设定的显著性水平（例如 0.05），就可以拒绝原假设，认为变量之间有显著的关联，或模型不适合数据。