ch１統計学とは

1.1 データを分析する

データ分析の目的：

• データを要約する、like average data
• 対象を説明する
  • 対象が持つ、関係性を明らかにし理解につながる。
  • 前提条件：すべての関係がない可能性を排除する必要があります。
  • 説明のレベル：因果関係、相関関係
  • 因果関係：二つのうち、一方の要因を変化させると、もう一方を変えることができる関係である。
  • for example:　新薬と血圧
  • 相関関係：一方が大きいと、もう一方も大きい（小さい）と関係。
  • for example:　年収と幸福度
• 未知のデータを予測する。

1.2 統計学の役割

• ばらつきがある(不確実性)データに立ち向かい、説明や予測を行う。
• 不確実性を対処する方法として：
  • 確率を使う

1.3 統計学の全体像

統計学を概観として、there are two types here.

• 記述統計：得られたデータを整理し要約する手法
• 推測統計：得られたデータからの発生元の対象を推測する統計手法。

推測統計

• 从数据推出模型，再用模型做预测就是推测统计。Step is like:

  1. data
  2. 確率モデル
  3. 予測・説明

• 推測統計には、二つある:

  • 統計的推定：データから仮定した確率モデルの性質を推定する方法，从样本推出总体特征

    • 比如，求全村人的平均年龄
      1. 先抽样
      2. 计算平均值
      3. 设置置信区间
      4. 然后比较得出结果

  • 仮設検定：立てた仮設と得られたデータがどれだけ整合するかを評価し、仮説を支持するかどうかを判断する手法である。

    • 假设检验

    • step

      1. 提出假设（H0，H1），H1是希望证明的假设，通常表明存在某种效应或者关联。

      2. 收集数据

      3. 确定检验方法（T检验，F检验之类的）

      4. 确定显著水平

      5. 和显著水平做比较，做结论，并解释结果。

Ch2 母集団を標本

2.1データ分析の目的と興味の対象

2.2 母集団(population)

• sizeにより、有限母集団と無限母集団ある。

2.3 母集団の性質

母集団の性質を知るために、以下の方法ある

1. 全数調査　　（分析するdata 　＝　母集団）、記述統計
2. 標本調査
   • 母集団の一部を分析することで、母集団全体の性質を推測する推測統計である
   • sample size is important in this situation

ch3　統計分析の基礎

3.1 data's type

• 変数
  • 量的変数：離散、連続
  • 質的変数（カテゴリ変数）： 分类变量，eg：geder 1/0

3.2 data distribution

• dataの可視化
  • 離散：
    1. 散点图 - Scatter Plot
    2. 柱状图 - Bar Chart
    3. 折线图 - Line Chart
    4. 盒须图 - Box Plot
    5. 饼图 - Pie Chart
    6. 热力图 - Heatmap
  • 連続:
    1. Line chart - 折线图
    2. Scatter plot - 散点图
    3. Curve chart - 曲线图
    4. Area chart - 面积图
    5. Bar chart - 柱状图
    6. Histogram - 直方图
    7. Kernel density estimate plot - 核密度估计图
    8. Box plot - 箱线图
    9. Heatmap - 热力图
    10. Contour plot - 等高线图

3.3 統計量

データの性質を要約するための統計量を記述統計量また要約統計量と呼ぶ。

• 記述統計量（descriptive statistics）（描述数据基本特征）
  • 平均値
  • 中央値（中位数）
  • 最頻値（众数）
• ばらつきを表す値（measure of dispersion）（表达离散程度）
  • 標準偏差（std）（standard deviation）、值越大，图像越扁

Attention：異常点！！！

分布を可視化する箱ヒゲ図

• 最小值：Q1 - 1.5 * IQR

• 第一分位(Q1)

• 中位数(Q2)

• 第三分位(Q3)

• 最大值：Q3 + 1.5 * IQR

• IQR：对应数据分布最核心的位置，这里箱体长度越长，数据离散程度越大。

• 离群点


3.4 確率変数（随机变量）

P（X=赤玉）

確率分布

確率とは、横軸に確率変数を、縦軸に確率変数の起こりやすさを表した分布です。

離散：確率変数

連続：確率密度関数、这种情况下求概率就是求概率密度函数的面积，用scipy可以求

推測統計と確率分布

データはとある確率分布から得られた実現値であると考え

将数据视为从某个特定的概率分布中获得的实现值。

期待値E（X）

简单说就是平均值

分散と標準偏差

就是形容数据分散程度的

歪度和尖度

• 歪度（Skewness）衡量了概率分布的偏斜程度（左右对称作为标准）。
  • 如果数据更多地集中在分布的左侧，则歪度为负；
  • 如果数据更多地集中在分布的右侧，则歪度为正。
• 尖度（Kurtosis）衡量了概率分布曲线的尖峰程度。
  • 如果概率分布曲线具有较高的尖峰，尖度将是正的；
  • 如果概率分布曲线相对平坦，则尖度将是负的。

二つの確率変数を考える（联合概率分布）

• 独立

• 非独立

条件付き確率(条件概率)

3.5 理論的な確率分布

確率分布とパラメータ

就是模型和参数

正規分布

正态分布

• 平均を中心とした、左右対称の分布である
• 自然界分布基本都是正态

標準化(0,1)

ch4　推測統計〜信頼区間

4.1 全数調査と標本調査

データを得る方法について

母集団から一部を抽出する

確率分布と実現値

データから、その発生元である確率分布を推測する

就是从数据倒退模型

母集団分布のモデル化

無作為抽出（Random Sampling）

打乱数据再抽，不然肯定有偏差啊

無作為抽出の方法

• 単純無作為抽出法
• 層化多段抽出法

データの取り方

推測統計を直感的に理解する

• 本当に興味があるのは母集団です
• 小さいサンプルサイズの標本から」母集団を推測できる
• 標本を抽出する頭巾は、Random Sampling

4.2 信頼区間

母集団とデータの間の誤差を考える

• 求全部平均成本高
• 所以先抽样
• 从样本数据建模
• 根据模型推全体状况

標本誤差

样本退出来的平均，和真正的全数据平均的偏差就是标本误差

サイコロにおける標本誤差

六个面平均 ，和你摇骰子六次的平均就是标本误差。

大数の法則

样本量足够大时，标本误差接近0

標本誤差の確率分布を知る

標本誤差の確率分布がわかれば、どの程度の大きさの誤差が、どの程度の確率で現れるかを知ることができる。

中心極限（きょくげん）定理

当样本量足够大时，他们的平均值会服从正态分布

推定量

性质：

• 不偏性
• 一致性
• 有効性

举个栗子：

• 求全城人平均身高

• 先抽样，每组20人，抽10组

• 得到10组的平均值

• 再求这10组平均值的平均值，X

  • 如果，X = 总体平均值，叫不偏性

• 如果，任意两组A和B的平均值相等

  • 但A组方差更小，也就是说，更集中 ，则A组的有效性比B组好

• 一致性：更强调过程

  • 随着样本数量的增大，统计量会趋于真实值。

標本誤差の分布

下图为标准误差的分布，其实就是个正态分布

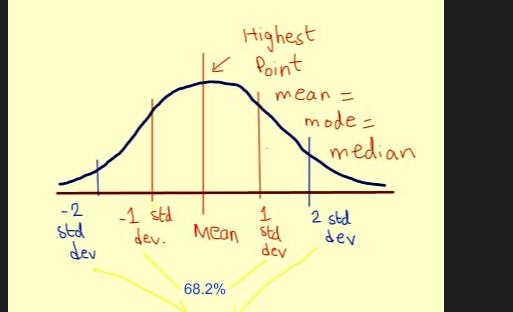
• 横轴是几倍的方差

• 倍数	概率
  1	68%
  2	95%
  3	99%

$$ \Large std = \sigma/\sqrt[]{n} $$

信頼区間の定義

〇〇％信頼区間の解釈は、「〇〇％の確率で、この区間が母集団平均μを含んでいる」となる。

t分布と95％信頼区間

t分布

在进行t检验时，有几个假设前提需要满足：

• 总体分布假设：t检验要求数据符合正态分布。通常在样本较小（N<30）的情况下，使用t检验。

• 独立性假设：t检验要求样本之间是相互独立的。这意味着每个样本的观测值不受其他样本的影响。

• 方差齐性假设：在一些情况下，t检验还要求待比较的两个样本具有相等的方差，这称为方差齐性。但在实际应用中，如果样本量相等且相差不大，则方差齐性的假设可以放宽。（验证方差是否相等，巴特利特检验，见ch6.2）

t检验由于通常在小样本量的情况下使用，因此画出的图很扁，方差大。

95％信頼区間

	正規分布	t分布
正	1.96	2.26
負	-1.96	-2.26

精度を高めるためには

標準誤差stdを小さくするためには、分子の標本標準偏差sを小さくすることができるが、一般的に難しい。だから、分母のサンプルサイズnを大きくさせる。

ch5 仮説検定

5.1 仮説検定の仕組み

推測統計はもう一つの手法

仮設検定では、P値という数値を計算し、仮説を支持するかどうかを判断する。

仮説の検証

• 仮設検証型データ：仮説を立ってから、データ分析。
• 探索型データ：仮説なかったままに、データ分析。

仮設検定

1. 仮説を立つ
2. groupを分ける
   • 処理群（treament group）
   • 対照群(control group)

統計学における仮説とは

帰無仮説と対立仮説

• 帰無仮説：示したい仮説の否定命題。（H0）、例えば、新薬が効果ない
• 対立仮説：示したい仮説。（H1）、例えば、新薬効果ある
• 原假设(又称零假设)，是假定总体参数未发生变化；备择假设(又称对立假设)，是假定总体参数发生变化。

母集団と標本の関係再び

就算两组标本的平均数完全相等，两组母集团的数据也很可能不相等。因为抽样是有误差的。

帰無仮説が正しい世界を想像してみる

都是先假设归无假说成立的，比如你不能轻易就说一个新药有效，肯定是先假设他无效，在假设的极端情况下有效才是真有效。

P值

p 值表示极端情况下出现的概率，p不在信赖区间内，即p<0.05（比如说p大于3倍标准差），也就是说在我假设新药无效的前提下，新药有效的极端概率还是有99%，那这种情况下当然可以说新药有效，即拒绝归无假说，接受对立假说。

仮設検定の流れのまとめ

5.2 仮設検定の実行

仮設検定の具体的な計算

• t検定：２群間の比較
• 棄却域：有意水準１％、5％、１０％
• 両側検定、片側検定

5.3 仮設検定に関わるグラフ

Error Bar

https://www.sohu.com/a/113524082_177233#google_vignette

举个栗子：

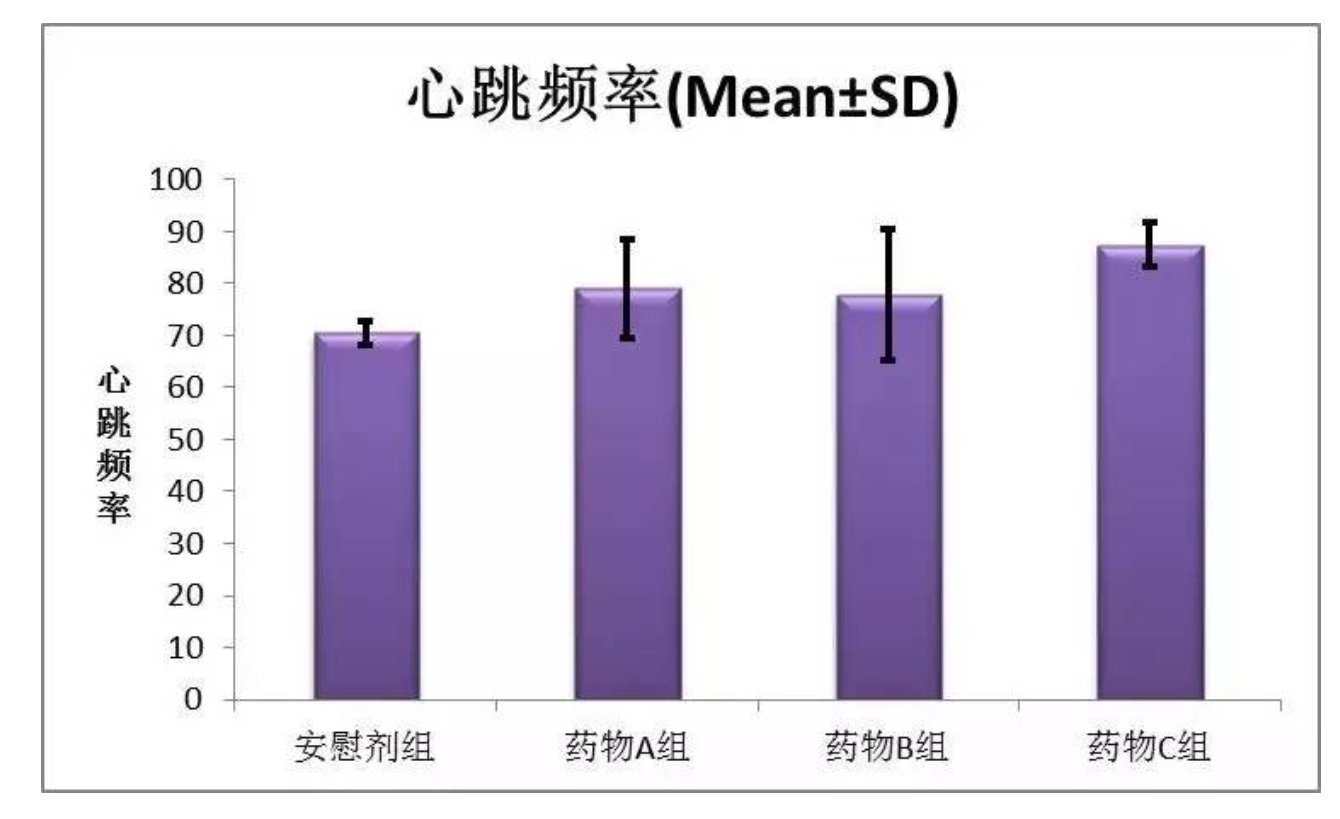
黑线上下的就是正负标准差，紫色的那个位置就是平均值。

5.4 第一種の過誤と第二種の過誤

真実と判断の４パターン

第一種の過誤（α）

ほんとは、差がない、差があると判断する。

p値と有意水準から第一種の過誤を起こす確率をコントロールすることができる。

H0为真，但拒绝了H0（不管H0怎样，都拒绝H0）

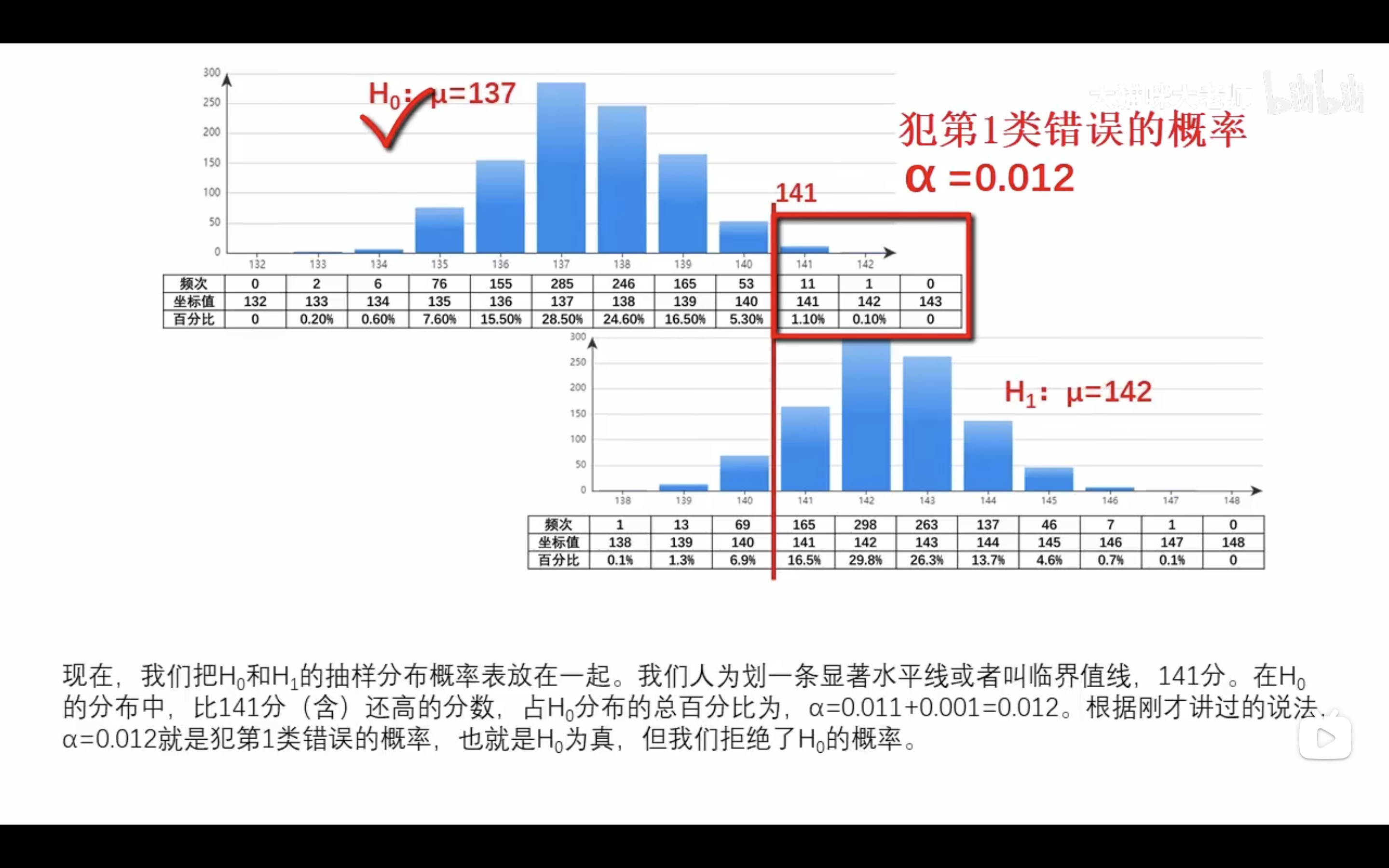
第二種の過誤（β）

ほんとは、差がある、差がないと判断する。

H0为假，但接受了H0。（不管H0怎样都接受H0）

如下图

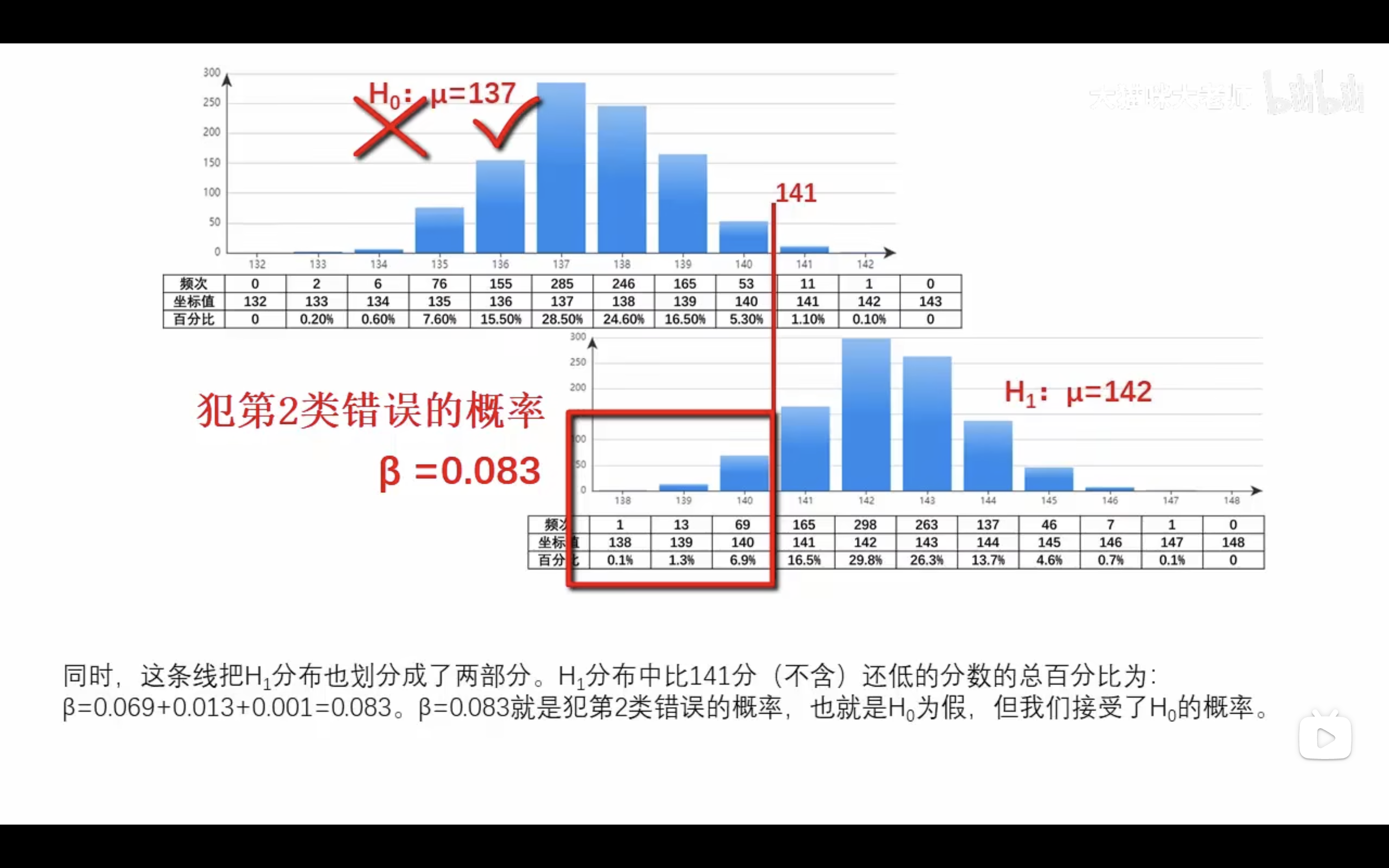
αとβは　trend offの関係

• α：第一種の過誤を起こす確率
• β：第二種の過誤を起こす確率

这俩值一个变大，另一个一定会变小。

ch6 様々な仮設検定

6.1 様々な仮説検定

仮設検定手法を使い分ける

仮設検定は、二群の平均値の比較以外にも、様々な目的、仮設に対して実行できる。ただし、解析の目的やデータの性質によって手法が異なるため、注意が必要ある。

• t検定：sample size < 30　使う
• F検定：比较多个样本组之间的方差
• 卡方検定（かいニ乗）（Pearson's chi-squared test）：卡方检验通常用于比较观察值与期望值之间的差异。通常用于两种情况：拟合优度检验和独立性检验。

检验基本流程 （大体一致）

1. 设定零假设和备择假设
2. 根据样本数据计算统计量
3. 根据统计量判断选择零假设还是拒绝零假设

データのタイプ

データのタイプが量的変数かカテゴリ変数であるかにより、解析手法にが異なる。

• 分割表，

• 散布図

標本の数

標本の数も、解析手法の選択において重要なfactorである。

量的変数の性質

データに量的変数がある場合、データがどのように分布しているかは検定手法を選択際に重要である

• パラメトリック検定：母集団が特定の分布に従っていると仮定を置いた仮設検定である。
• ノンパラメトリック検定：母集団が特定の分布を仮定できない仮設検定である。
  • 比如：左右不对称的数据分布。
  • 或者，平均值，方差不起到判断使用什么分布作用时。如均值，方差相等。page135的图。

6.2 代表値の比較

一標本のt検定

只有一组标本量的t检验，这时候不是两组之间互相比较，而是主要调查母集团的平均值。

一標本のt検定设立的假说如下：

• 帰無仮説：「母集団平均はμ ＝＝ 〇〇」
• 対立仮説：「母集団平均はμ ！＝ 〇〇」

这时候这个平均μ怎么假设就很重要了

• 举个栗子：
• 直接说假设日本成年男性平均身高170，毫无意义。
• 但如果已知中国成年男性平均身高170的话，这是假设日本成年男性平均身高170就没有问题。

この場合、95％信頼区間を求めることと、α＝0．05の有意水準で帰無仮説検定を実施することは、 X̄　から考えるのか、帰無仮説μ ＝＝ 〇〇から考えるかの違いであり、表裏一体であることがわかる。

二標本のt検定

２標本t検定は、二つの群での平均値を比較する。

二標本のt検定设立的假说如下：

• 帰無仮説：「二つの群の平均値は等しい」
• 対立仮説：「二つの群の平均値は等しくない」

対応のない検定、対応のある検定

就是抽样样本之间没有映射关系，比如说验证药物是否有效

• 対応ない検定：抽两组人，一组喝药后测血压，一组不喝药测血压。两组人之间没有映射关系

  • ２標本のt検定
  • 第二種の過誤が起きやすい。

• 対応ある検定：抽一组人，喝药前测血压，喝药后测血压。自己就是两组实验的映射关系。

  • 1標本のt検定
  • 第二種の過誤が起きにくい。

正規性を調べる

シャピロ ウイルク検定

Shapiro-Wilk检验是一种用于检验数据是否来自正态分布的统计方法。它通过计算样本数据与正态分布的拟合程度来进行判断。Shapiro-Wilk检验通常用于小样本数据，对于大样本数据，其他方法如Kolmogorov-Smirnov检验可能更适用。

Shapiro-Wilk检验假设如下：

• 帰無仮説：「母集団の分布が正規分布である」
• 対立仮設：「母集団の分布が正規分布ではない」

等分散性を調べる

バオートレット検定

巴特利特检测（Bartlett test）是一种用于检验各组方差是否相等的统计检验方法。它通常用于方差分析（ANOVA）前的检验，以确保各组样本的方差是否具有统计学上的显著差异。这个检验的原假设是各组样本的方差相等。如果巴特利特检验的结果显示各组方差不等，则可能需要采用调整后的统计分析方法来处理数据。

Bartlett test检验假设如下：

• 帰無仮説：「全ての群に対して母集団の分散が等しい」
• 対立仮設：「全ての群に対して母集団の分散が等しくない」

ノンパラメトリック版の２標本の代表値比較

• 各群のデータに正規性がない場合に、ノンパラメトリック検定に分類される手法を使う。

• この場合、平均値の代わりに、分布の位置を示すために、ウィルコクソンの順位和検定

ウィルコクソンの順位和検定(Wilcoxon rank sum test )

• Wilcoxon秩和检验是一种非参数统计检验方法
• 用于比较两个独立样本的总体中位数是否相等。
• 它可以用来替代独立样本的t检验，特别是当数据不满足t检验的假设（如数据不服从正态分布）时。
• Wilcoxon秩和检验基于样本的秩次而不是实际的观测值，因此对于一些数据类型更具有鲁棒性。

Wilcoxon秩和检验假设如下：

• 帰無仮説：「二つの母集団の位置が同じである」
• 対立仮設：「二つの母集団の位置が異なる。」

三群以上の平均値の比較

分散分析（Analysis of variance）を用いる。

• 方差分析是一种统计方法，用于比较两个或多个组的平均值是否有显著差异。
• 特别是想要了解不同组之间是否存在显著差异时。
• 方差分析将数据分解成组内方差和组间方差两部分，通过比较它们的大小来确定组间差异的显著性。
• 这种方法通常用于比较三个或更多个组的平均值，例如不同治疗方法的效果是否有显著差异。

ANOVA设立的假设如下：

• 帰無仮説：「全ての群の平均が等しい（μa = μb = μc）」
• 対立仮設：「少なくとも一つのpairに差がある」

Attention:拒绝零假设，只能说明三组之间平均值存在差异，不能说明具体哪两组存在差异，需要进一步验证

分散分析の仕組み

举个栗子：

• 现有三个专业医学，数学，生物的学生，要验证他们的推理能力是否相等
• 零假设：三个专业学生推理能力相同
• 备择假设：至少存在一组学生推理能力不相等。
• 如果方差分析结果拒绝零假设，则只能说明三组学生的推理能力不同，不能说明具体哪两个专业的学生存在差异，需要进一步验证

自由度

自由に変動できる変数である

为什么标准差的自由度是n-1

• 因为计算标准差需要平均值，也就是说此时平均值已经确定。
• 一共三个人，平均每人两碗饭，前两个人可以自由选择，第三个人没得选。
• 所以计算方差的自由度只有n-1，因为平均值是已经确定了的了。

多重比較

群の数が増えるほど、第一種の過誤が起こりやすい。

6.3 割合の比較

Binomial Distribution (Bernoulli )二項分布

カイニ乗検定：適合度検定（Pearson's chi squared Test）

Pearson's chi squared Test检验假设如下：

• 帰無仮説：「母集団の分布は想定している離散確率分布である」
• 対立仮設：「母集団の分布は想定している離散確率分布ではない」

カイ二乗検定の独立性の検定

检验假设如下：

• 帰無仮説：「二つの変数は独立である」
• 対立仮設：「二つの変数は独立ではない」

卡方分布

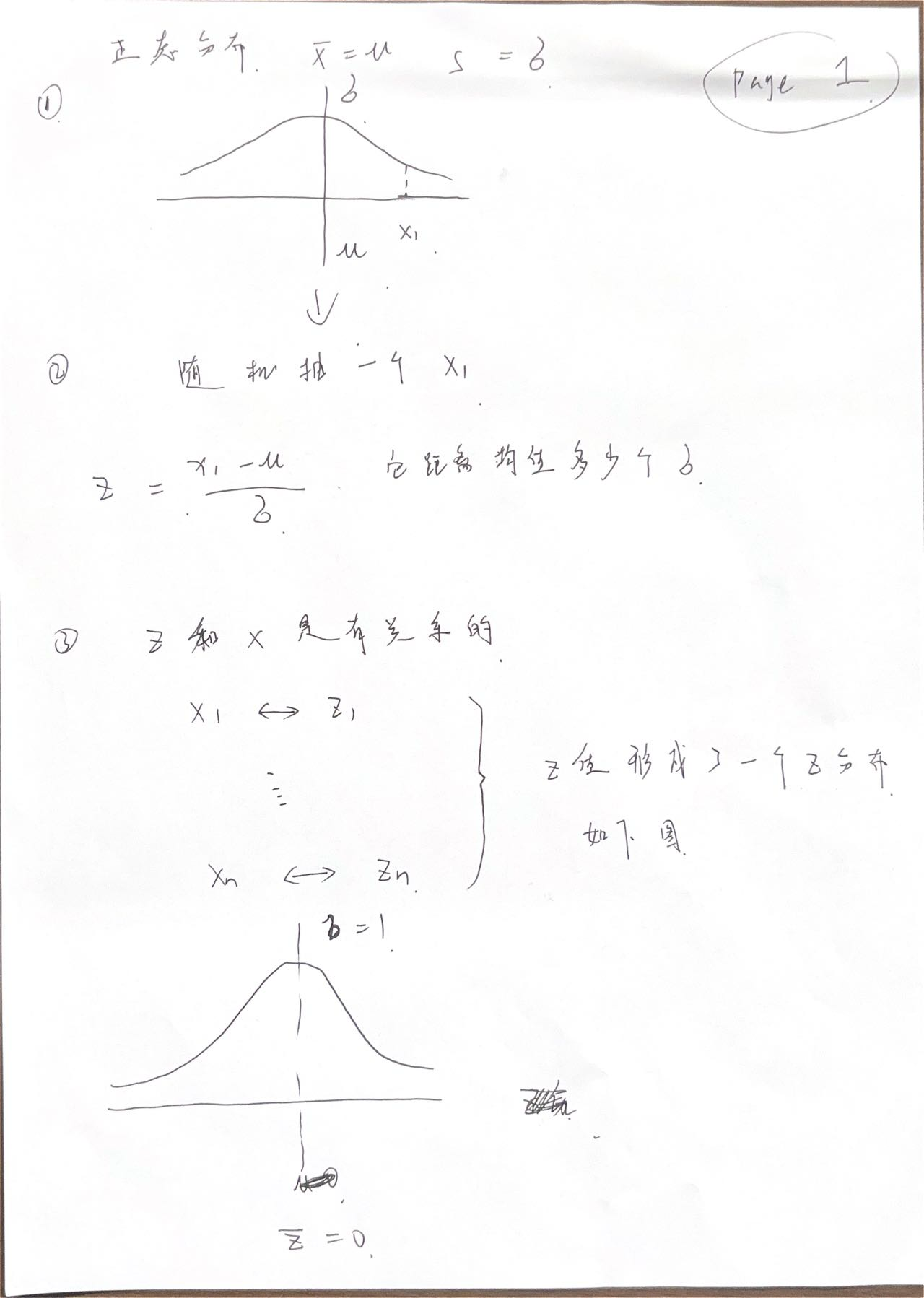
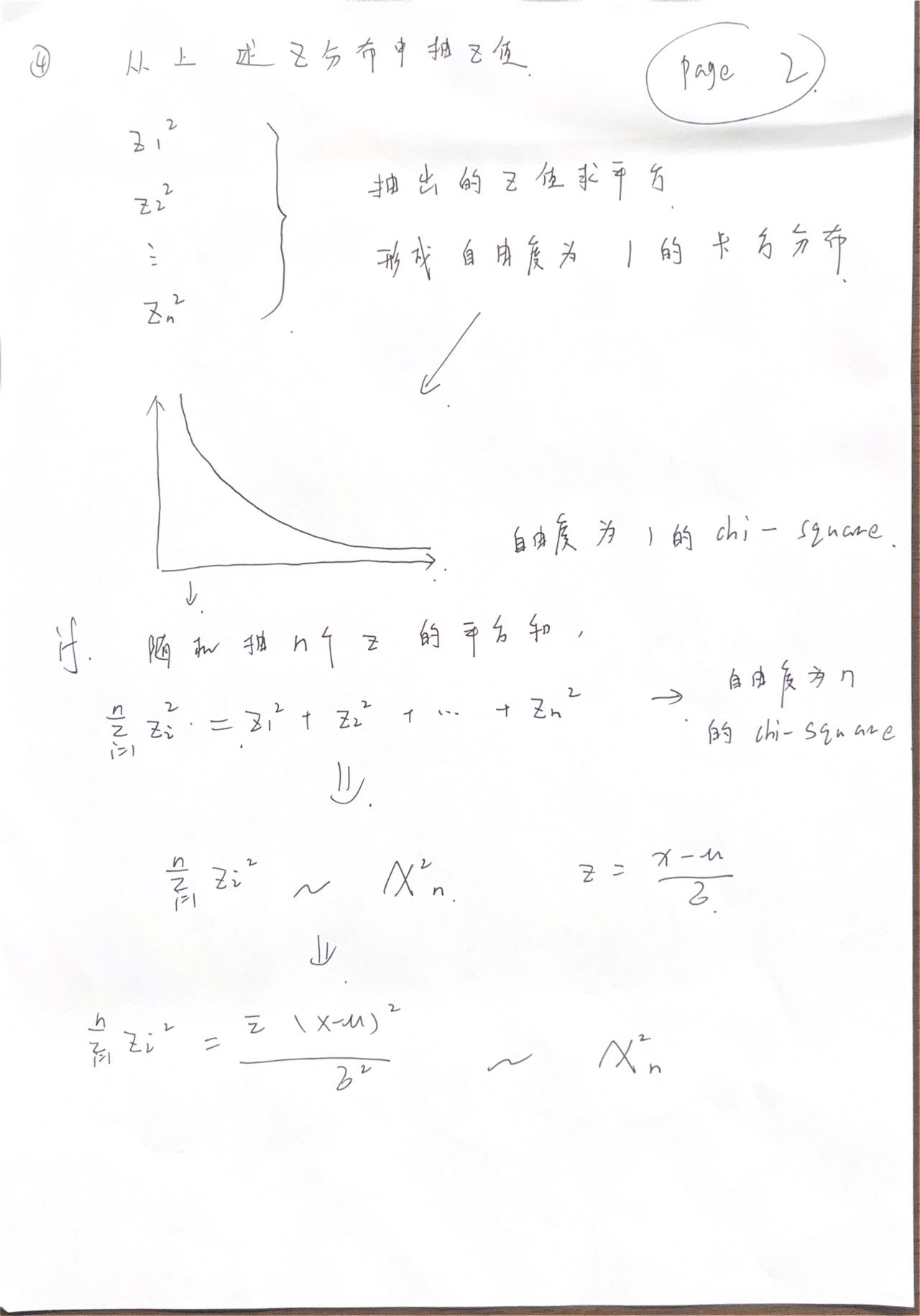
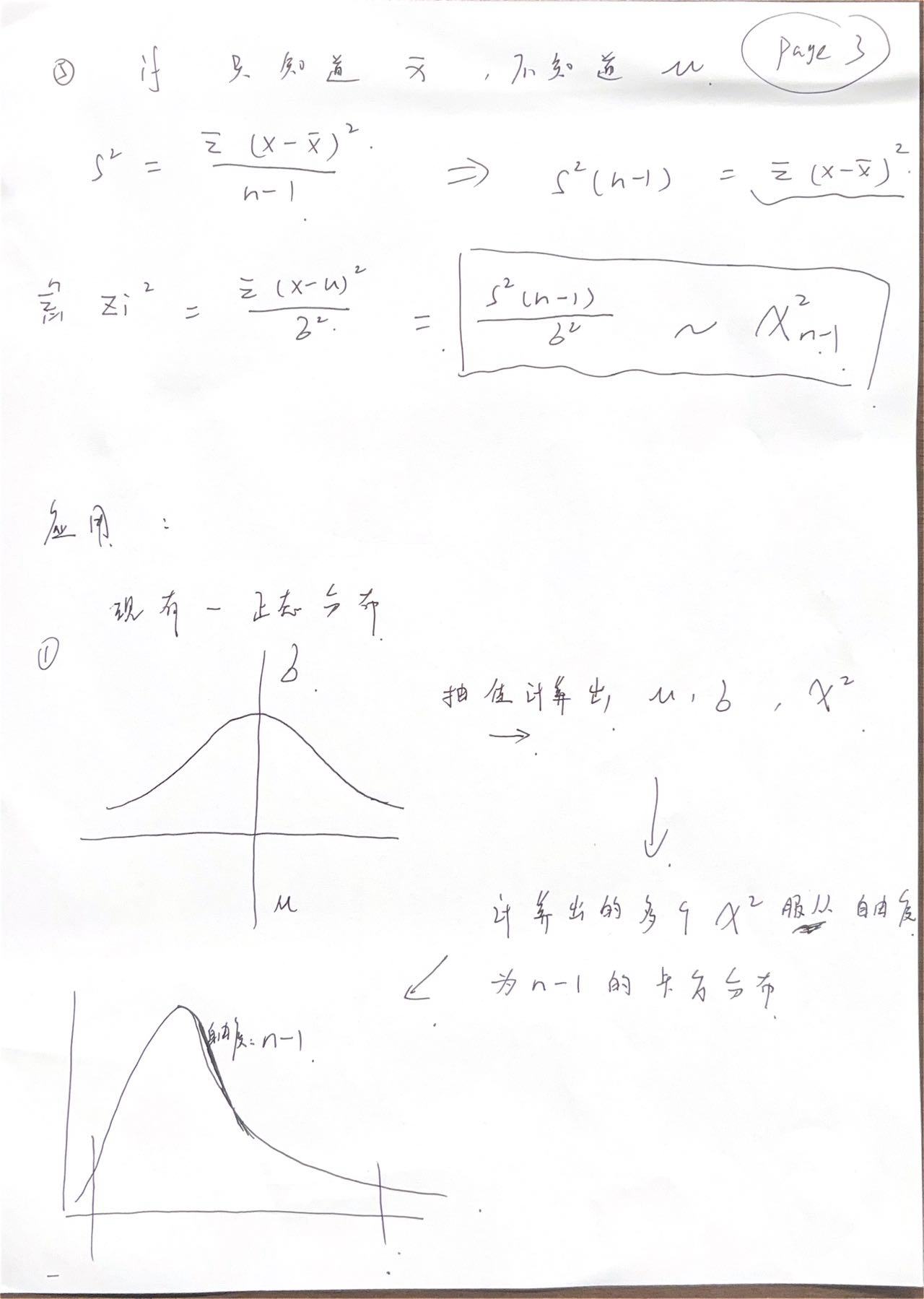
ch7 回帰と相関

7.1 量的変数同士の関係を明らかにする

二つの関係がある：

• 相関
• 回帰

散布図（scatter plot）

像大致看一下连续数据之间的关系，先画一个散点图。

相関(correlation)

• 相关性是用来衡量两个变量之间的关联程度，通常使用相关系数来表示。相关系数的取值范围在-1到1之间，-1表示完全负相关，1表示完全正相关，0表示无相关性。
• 相关性分析主要关注的是两个变量之间的线性关系强弱以及方向，但不涉及因果关系。
• 相关性分析不涉及对因果关系的推断，仅用于描述两个变量之间的关联程度。

回帰（Regression）

• 回归分析是用来探究一个或多个自变量对因变量的影响程度，并建立一个预测模型的方法。回归分析可以是简单线性回归（只涉及一个自变量）或多元线性回归（涉及多个自变量）。
• 回归分析旨在通过对自变量和因变量之间的函数关系进行建模，来解释和预测因变量的变化。在回归分析中，通常使用拟合优度等指标来评估模型的拟合程度。
• 回归分析可以用于因果推断，即确定自变量与因变量之间是否存在因果关系。

7.2 相関係数（Pearson's correlation coefficient）

https://juejin.cn/post/7196290097549361209?searchId=20240422091603FB79619045A68D03E7FD（代码）

分以下两种情况：

• 正态分布：使用pearson系数r
• 非正态分布：使用spearman系数ρ

正态分布：ピアソンの積率相関係数r

• 计算r的前提是必须是正态分布。

• 皮尔逊系数落在[−1,1]

• 绝对值越接近1，相关性越强，符号代表正相关或负相关

相関係数rは線型な関係を捉える。

rは二つの量的変数の間における関係の強さを定量化する手法を説明する**、しかし、線の傾きの大きさと関係がない。**

非正态分布：

スピアマン順位相関係数ρ，（n>30）

https://juejin.cn/post/7195433939593330749?searchId=20240422091501D49AA5F3CD4678F8AB0B（代码）

kendall rank correlation coefficient：n极端小时使用

https://juejin.cn/post/7187943854141046839?searchId=202404220917070B3E9D8E41C4A8FEFFCC（代码）

相関係数の仮設検定

相関係数の有意性の検定：

• 帰無仮説：「r == ０」
• 対立仮設：「r != 0」

就算算出来的相关系数不等于0，但如果相关系数的检验没有通过，也就是说p>0.05时，也不能说r不等于0。即相关性检验不通过，不能说两变量具有相关性，即使计算出的相关系数不为0.

サンプルサイズと仮説検定

• 当n特别大时，且数据间存在若相关关系时，有可能会因为偏差，算出p值<0.05，而导致误判r==0，即没有相关性。

• 解决方案：同时计算p值和r值

非線型相関

情報量に基づいた指標がいくつか提案されている。

7.3 線型回帰

回帰分析の概要

最小二乗法（least square）

残差の二乗の総和が最小になるように係数を決める。

回帰係数

回帰係数の仮設検定

95％信頼区間

推定された回帰直線の周りに影を書くことで、回帰直線の95％信頼区間を書いている。

意味：同様の標本抽出と回帰分析を100回行ったら、100回のうち95回ほど、この範囲に母集団のモデルを含んでいることを意味する。

95% 予測区間

95％信頼区間 <=> 95% 予測区間

決定係数（R square）

適合度を表す。１に近く　、適度が良くなる

表明了拟合优度，数值越接近1，拟合程度越好

調整済みR square

"adjusted R" 指的是调整后的 R 方（R-squared），它是多元线性回归模型中的一个统计量，用于衡量模型对观测数据的拟合程度。与普通的 R 方类似，调整后的 R 方考虑了模型中自变量的数量，以避免过度拟合的问题。

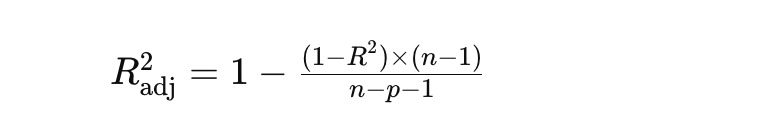
其中，n是样本数量，p是模型中的自变量数量

誤差の等分散性と正規性

看183页的图就知道了，很难说。

説明変数と目的変数

説明変数と非説明変数：因果関係を表す

ch8　統計モデリング

8.1 線型回帰から広い枠組みへ

線型回帰はさまざまな解析手法の基礎

• 重回帰

重回帰

系数的日语叫偏回帰変数

重回帰の結果の見方

• 在多重回归分析中，标准误差（Standard Error）和系数之间存在密切的关系,标准误差是回归系数的估计标准偏差，用于衡量该系数估计的精确性。系数估计的标准误差越小，意味着该系数估计越精确，也就是说，该系数的真实值与样本估计值之间的不确定性越小。

標準化偏回帰係数

回归系数之间要想相互比较的话，要使用数据标准化之后求出的模型系数，也就是标准化偏回归系数。

偏回帰係数の解釈

偏回归系数是去除了多重共线性影响的系数，可以放心使用

説明変数はカテゴリに

カテゴリには大小関係がないので、回帰分析の説明変数に用いる場合には、０or１のダミー変数として説明変数を導入する必要がある。

カテゴリが三つ以上の場合

sklearn　可以解决

共分散分析（ANCOVA）

协方差分析

共変量（covariate）：协方差是统计学中用来衡量两个随机变量之间的关系的指标，表明两个变量之间的相关关系，绝对值越大，相关关系越强，正负代表正相关还是负相关

相关系数：标准化后的协方差。【-1，1】，越接近1，相关性越强，正负代表正相关还是负相关

高次元データにおける問題

次元が高くなると、多重共線性の問題が起きやすくなる、モデルの精度も悪くなる。解決ために、PCAとか使える。

多重共線性

就是模型内变量之间存在相关关系。

分散拡大係数(variance inflation factor)

表达两变量间相关程度的值，R square 越大，VIF越大

ViF 越大（大于10），变量间相关性越强。

8.2 回帰モデルの形を変える

交互作用（こうごさよう）

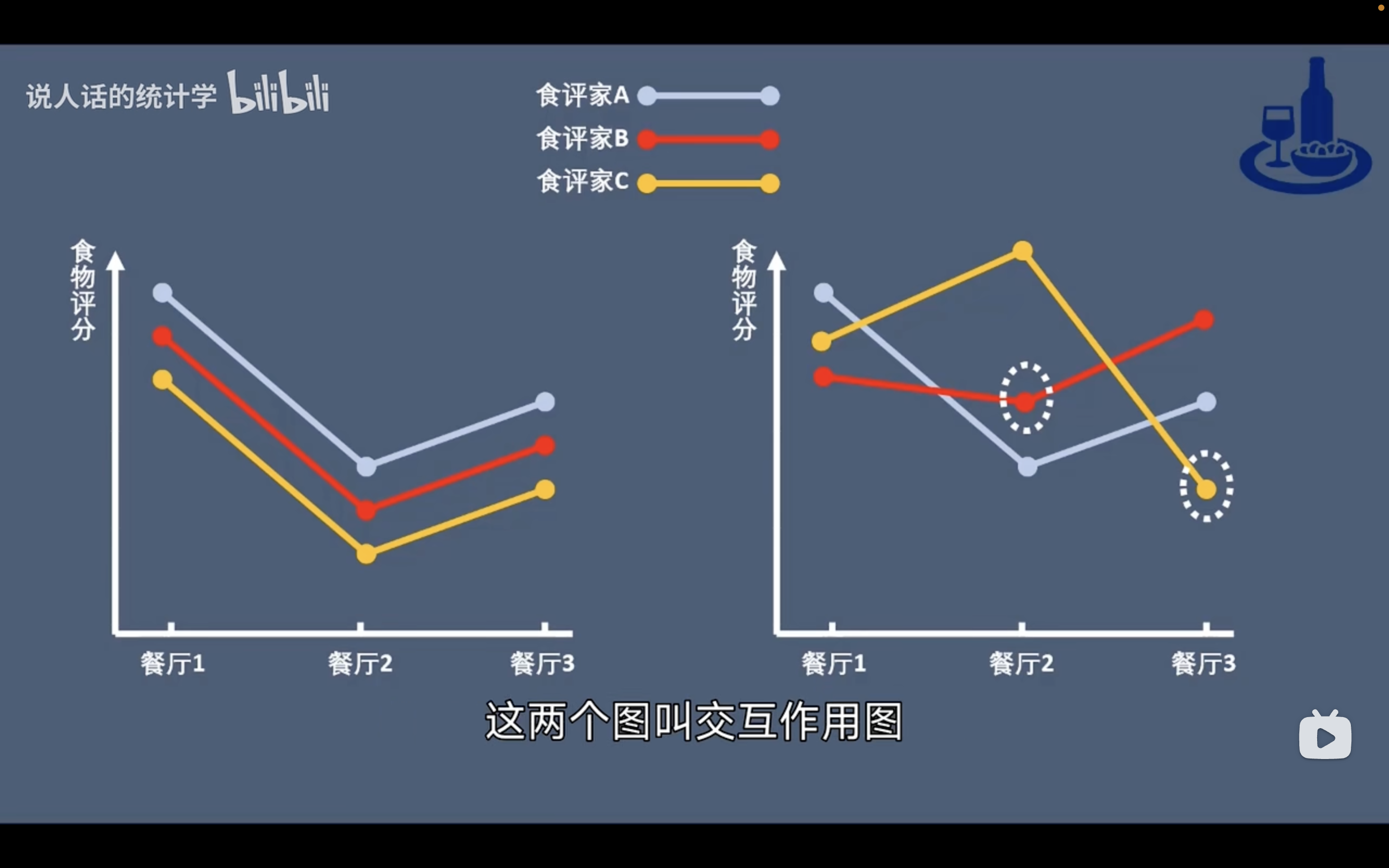
変数間の同士の相乗効果を交互作用という。

非線型回帰

8.3 一般化線型モデルの考え方

線型回帰の枠組みを広げる

一般化線型モデルの枠組みで、確率分布をきちんと考慮してモデル化することが必要になる

尤度と最尤法（似然和极大似然法）

尤度は、与えられたモデルの下で観測されたデータの妥当性や信頼性を評価します。

尤度関数は通常、既知のサンプルデータからモデルのパラメータを推定するために使用されます。

是的，似然函数通常用于从已知的样本数据中推断模型的参数。在统计学中，我们通常根据观察到的数据来估计模型的参数，似然函数提供了一种衡量观察到的数据在不同参数值下出现的可能性的方式。

具体来说，似然函数是关于模型参数的函数，它衡量了在给定模型下观察到的数据出现的可能性。我们的目标是找到使得观察到的数据出现的可能性最大化的参数值，这个过程称为最大似然估计（MLE）。换句话说，最大似然估计通过选择使得观察数据的尤度最大化的参数值来估计模型的参数。

因此，似然函数提供了一种从已知的样本数据中反推模型参数的方法。通过最大化似然函数，我们可以获得对模型参数的估计值，使得观察到的数据在给定模型下出现的可能性达到最大。

ロジスティク回帰（Logistic Regression）

逻辑回归和线性回归的区别

• 线性回归：线性回归是一种用于建模自变量和连续因变量之间关系的统计方法
• 逻辑回归：逻辑回归则是一种用于建模自变量和二元因变量之间关系的统计方法
• sigmod函数：可以预测二分选项的概率，逻辑回归的核心就这公式

Sigmoid函数是logit函数的反函数，变个型就得到了。

二项分布（Binomial Distribution）

• 離散データ
• μ = Np, σ = NP(1-p)
• 

Logit関数

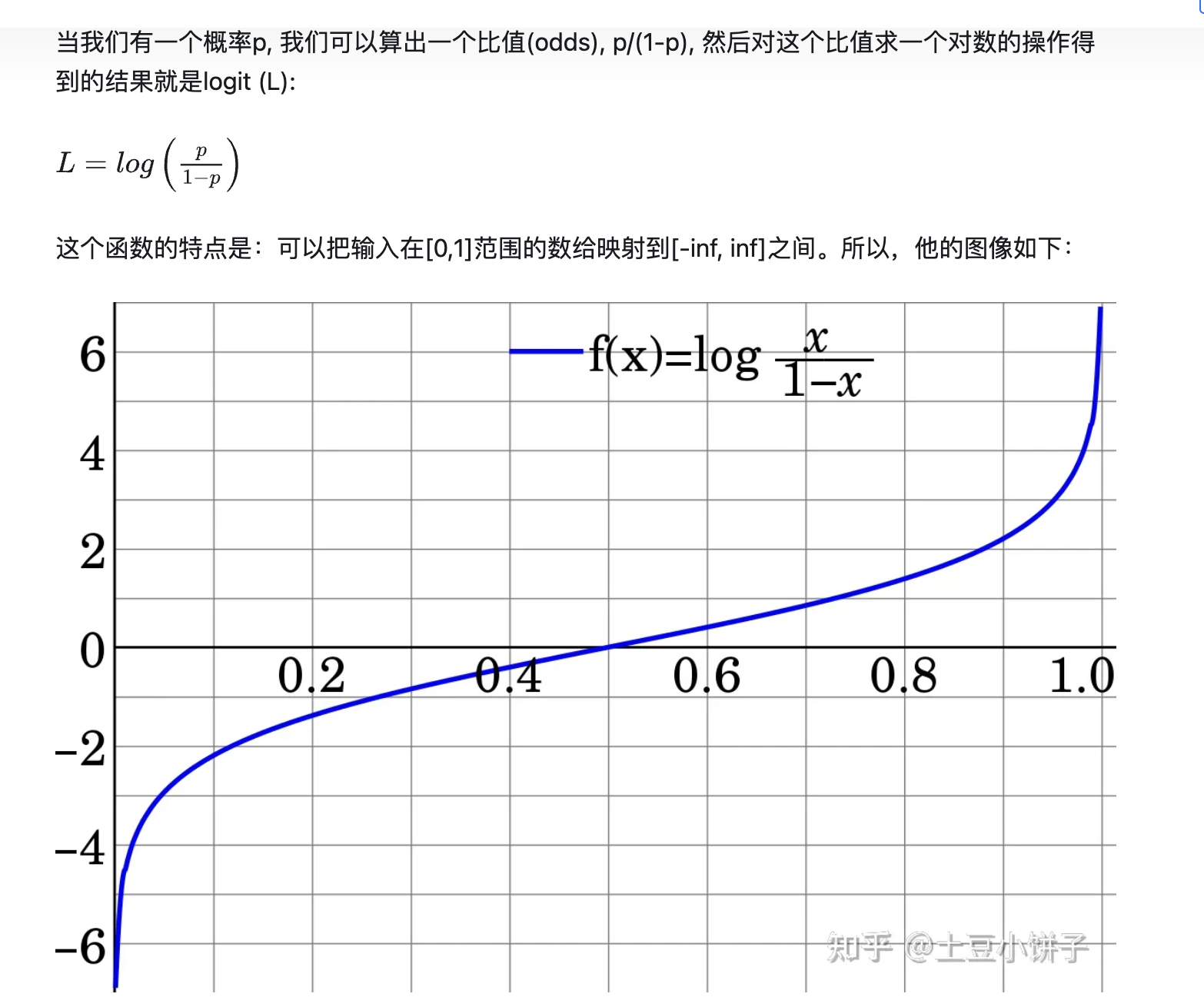
• 定义域：
  • y ∈ [0,1]
  • x ∈ [- ∞，+ ∞]

（オッズ比）odds ratio

ポアソン回帰（Poisson Regression）

【泊松分布是怎么来的？应该怎么用？】 https://www.bilibili.com/video/BV1B54y1s7Ud/?share_source=copy_web&vd_source=51cc2cdad73ec82b95881f9d39cacb48

• 一定时间内 ，某事件发生λ次的概率

• 

• 从二项分布的公式推导而来的，平均值和方差都为𝜆，𝜆越大 越接近正规分布。

• 举个例子：

• 假设某个地区的某种事件平均每天发生 3 次，我们想要计算发生 5 次这种事件的概率，可以使用泊松分布的概率质量函数来计算。

# 假设某个地区的某种事件平均每天发生 3 次，我们想要计算发生 5 次这种事件的概率，可以使用泊松分布的概率质量函数来计算。

# 泊松分布的参数为𝜆， λ是事件发生的平均次数，这里是3。

# 我们将 k 设置为 5，表示我们想要计算发生 5 次事件的概率。


𝑃(𝑋=5)=𝑒−3×355!*P*(*X*=5)=5!*e*−3×35

𝑃(𝑋=5)=𝑒−3×355×4×3×2×1*P*(*X*=5)=5×4×3×2×1*e*−3×35

𝑃(𝑋=5)≈0.0498×243120*P*(*X*=5)≈1200.0498×243

𝑃(𝑋=5)≈12.084120*P*(*X*=5)≈12012.084

𝑃(𝑋=5)≈0.1007*P*(*X*=5)≈0.1007

因此，发生 5 次这种事件的概率约为 0.1007，或者约为 10.07%。

一般化線型混合モデル（GLMM）

固定効果：杀虫剂量，共通的

random效果：不同的山，不同的

8.4 統計モデルを評価、比較する

三大检验

wald検定

wald = 尤度/方差

但在n<30时，GLMM 模型的wald检定不准，所以这时候使用尤度比检定

尤度比検定（Likelihood Ratio Test ）（LR检验）

书上的：

• 帰無仮説：y＝a,(b=0)
• 対立仮設：y=a+bx,(b!=0)
• 検定統計量が大きいほど、帰無仮説に比べて対立仮説の尤度が大きく、モデルが改善することを意味する

我的：

• 目的：根据数据得出的模型有许多参数，想看模型和数据拟合的好不好，主要看这些参数准不准确，可以用LR检验来看。
• 假设两个模型做对比，一个复杂模型，一个简单模型：
  • H0:一个简单模型， y＝a
  • H1:一个复杂模型 y=a+bx
  • D = -2*（log（L1/L2））
    • L1/L2 > 1 ,简单模型更好
    • L1/L2 < 1, 复杂模型更好

贝叶斯统计

AIC（Akaike Information Criterion）（赤池情報量基準）

• 越大模型效果越差，越小越好

BIC

越大模型效果越差，越小越好

DIC

这三个都是检验模型好坏的，数值都是越小越好

Lagrange Multiplier Test （LM检验）

• 拉格朗日乘数法检验

ch9 仮設検定における注意点

9.1 再現性

• 低い再現性をもたらす主な原因の一つは、仮設検定の使い方である
• P-hacking:p値が０.０５を下回るように操作することができる

p-hacking的操作手法（一小部分）：

• 实验结束后追加样本量N

9.2 仮設検定の問題点

Fisher's Exact Test（费舍尔精确检验)とpearson's Test

• Fisher's Exact Test（费舍尔精确检验):只关注p
• pearson's Test：同时关注p和N，但不是所有情况N都是可控的

Sample Size N

• 实验结束后追加样本量N是不行的，要在设计实验阶段就确定N
• α、1-β、効果量を決めれば、Nを計算できる

代码

https://zhuanlan.zhihu.com/p/309323103

statsmodels文档：

https://www.w3cschool.cn/doc_statsmodels/dict.html 英文

https://www.heywhale.com/mw/project/60960b0364d3a200172540c0 中文

Sample Size n and p-value

Larger the sample，smaller the p-value

効果量（Effect　Size ）

Cohe's d

Meta-analysis

书上没细说，遇到了再研究

様々な効果量

• 分散説明率（Explained Variance ratio）:可以用来衡量PCA的效果，
  • 书上写的是按和R square一样想就行

ベイズファクター（Bayes factor）

周辺尤度（Marginal Likelihood）(边缘似然)

主要用来比较两个模型的效果

计算贝叶斯因子涉及对两个或多个模型的边际似然进行比较。具体的计算方法取决于所使用的模型和数据。这里我将提供一个简单的例子，假设我们比较两个线性回归模型的贝叶斯因子。

假设我们有两个线性回归模型：

1. 模型 M1: 𝑦=𝛽0+𝛽1𝑥+𝜖1y=β0+β1x+ϵ1
2. 模型 M2: 𝑦=𝛽0+𝛽1𝑥+𝛽2𝑥2+𝜖2y=β0+β1x+β2x2+ϵ2

我们假设观测数据 𝑦y 和 𝑥x 已经准备好了。

import numpy as np
import pymc3 as pm

# 模型 M1: y = beta0 + beta1*x + epsilon1
with pm.Model() as model1:
    beta0 = pm.Normal('beta0', mu=0, sd=10)
    beta1 = pm.Normal('beta1', mu=0, sd=10)
    sigma1 = pm.HalfNormal('sigma1', sd=1)
    mu1 = beta0 + beta1 * x
    y_obs1 = pm.Normal('y_obs1', mu=mu1, sd=sigma1, observed=y)

# 模型 M2: y = beta0 + beta1*x + beta2*x^2 + epsilon2
with pm.Model() as model2:
    beta0 = pm.Normal('beta0', mu=0, sd=10)
    beta1 = pm.Normal('beta1', mu=0, sd=10)
    beta2 = pm.Normal('beta2', mu=0, sd=10)
    sigma2 = pm.HalfNormal('sigma2', sd=1)
    mu2 = beta0 + beta1 * x + beta2 * x**2
    y_obs2 = pm.Normal('y_obs2', mu=mu2, sd=sigma2, observed=y)

# 计算模型 M1 和 M2 的边际似然
with model1:
    trace1 = pm.sample(2000, tune=1000)

with model2:
    trace2 = pm.sample(2000, tune=1000)

marginal_likelihood1 = np.exp(model1.logp(trace1).sum())
marginal_likelihood2 = np.exp(model2.logp(trace2).sum())

# 计算贝叶斯因子
bayes_factor = marginal_likelihood1 / marginal_likelihood2
print("Bayes Factor: ", bayes_factor)

如果计算出的贝叶斯因子为1，也就是两个模型效果差不多的时候，那就选择参数少的更为简单的模型。

論文が誤っている確率

• 偽発見率（FDR：False Discovery Rate）、FDRが高いことは再現性の低下に直結する。

• 立てた仮説が正しい確率をQとする。

• 仮設検定において良い仮説（高いQ）を立てることが、大切である。

9.3 p-hacking

• HAEKing:(Hypothesis After the Results are Known),

  • データを得て結果を見てから仮説を作ることである。

• 事前登録：

  • preregistration
  • 研究を実施する前に、研究計画として仮説と実験デザイン、解析手法を登録しておくことである。
  • 得られたデータを見てから仮説を立てるHARKingを防ぐことができる。

ch10

10.1 因果と相関

• 因果関係：原因の変数を変化させると、結果の変数を変える。
• 相関関係：二つの変数X、Yの間の関連性がある、そのため、一方の変数から、もう一方の変数を予測する可能にする。

交絡（confounder）：因变量和自变量の両方に関連するような外部の変数である。

解决confounder的方法：

• RCT（Randomized Control Trial）
• 重回帰
  • 把confounder factor 也作为一个变量加入回归方程里，看系数
• Score Matching
  • 比如同年龄，吃了药的实验组，和没吃药的对照组，的效果做对比，就是排除了confounder的结果

因果ー相関ー擬似相関

• 擬似相関：因果関係がないが、相関関係がある

• 不能说没有因果关系就一定有相关关系，有一小部分没有。

  • 举个例子：早上喝水，中午头疼。喝水既不是因果也不是相关，感冒可能才是。

時間（年齢）は交絡因子になりやすい

比如，同一个店铺，设置广告的时间和没设置广告的时间比较，得出广告提升了销量的结论中，时间因素就是confounder

RCT（Randomized Control Trial）

因果関係の根本的な問題は、個体の因果関係の効果がわかることができない

所以rct，然后关注群体的因果的平均效果。

Selection Bias

抽样的时候不够平均，比如全抽的男的

統計的因果推論

重回帰

• 可以用来解决confounder

重回帰

• 把confounder factor 也作为一个变量加入回归方程里，看系数

層別解析

傾向Score Matching（）

原因の変数＝０の群と、原因の変数＝１の群から、似た交絡因子を持つデータを見つけてペアにする。

差分的差分 DID（DIfference of Difference）

• 主要是为了考虑时间推移的影响
• 先假设对照组和实验组
• 其中对照组按时间，去两组数据y_control_1，y_control_2
• 实验组同样按照时间，y_treat_1，y_treat_2
• y_treat_2 减去 y_treat_1 得到的结果，同时混杂着时间因素和政策因素。

假设前提

假设前提：DID有一个很重要且很严格的平行趋势假设，即实验组和对照组在没有干预的情况下，结果的趋势是一样的。

代码

https://cloud.tencent.com/developer/article/2325287 腾讯的

准备数据

from faker import Faker
from faker.providers import BaseProvider, internet  # faker是用来创造虚拟数据的库
from random import randint
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import math
import statsmodels.formula.api as smf
import warnings

warnings.filterwarnings('ignore')

# 绘图初始化
%matplotlib inline
sns.set(style="ticks")

# 自定义数据
fake = Faker('zh_CN')
class MyProvider(BaseProvider):
    def myCityLevel(self):
      #随机返回一个城市类别
        cl = ["一线", "二线", "三线", "四线+"]
        return cl[randint(0, len(cl) - 1)]
    def myGender(self):
      # 随机返回一个性别
        g = ['F', 'M']
        return g[randint(0, len(g) - 1)]
fake.add_provider(MyProvider)

# 构造假数据，模拟用户特征
uid=[]
cityLevel=[]
gender=[]
for i in range(10000):
    uid.append(i+1)
    cityLevel.append(fake.myCityLevel())
    gender.append(fake.myGender())
    
raw_data= pd.DataFrame({'uid':uid,
                        'cityLevel':cityLevel,
                        'gender':gender,
                       })

raw_data['class'] = raw_data['uid'].map(lambda x: 'A' if x % 2 == 1 else 'B') # 按奇偶随机分组

# 构造did数据
df = pd.DataFrame(columns=['uid','cityLevel','gender', 'class', 'sales', 'dt'])
for i,j in enumerate(range(2005,2011)):
    lift = 1+i*0.05   #为了做一个偏差，
    df_temp = raw_data.copy()
    
    #np.random.normal()里面穿三个参数，平均值，方差，样本量size
    df_temp['sales'] = [int(x) for x in np.random.normal(300*lift, 60*lift, df_temp.shape[0])]
    
    # 假设因为政策冲击A组（实验组）销量将为88%
    df_temp['sales'] = df_temp.apply(lambda x: x.sales*0.88 if x['class']=='A' else x.sales, axis=1)
    
    #2007年之后，时间因素的影响对照组B的销量导致增加0.02
    if j>2007:
        df_temp['sales'] = df_temp.apply(lambda x: x.sales*(1+i*0.02) if x['class']=='B' else x.sales, axis=1)
    df_temp['dt'] = j
    df=pd.concat([df,df_temp])
    
df_did = df.groupby(['class', 'dt'])['sales'].sum().reset_index()

验证平行趋势假设

# 计算文字的y坐标
y_text = df_did.query('dt == 2007 and `class`=="B"')['sales'].values[0]
# 绘图查看干预前趋势
fig, ax = plt.subplots(figsize=(12,8))
sns.lineplot(x="dt", y="sales", hue="class", data=df_did)
ax.axvline(2007, color='r', linestyle="--", alpha=0.8)   # axvline函数表示画纵向虚线
plt.text(2007, y_text, 'treatment')
plt.show()

除了画图观察平行趋势，也可以通过回归拟合，参考自https://www.yisu.com/jc/614478.html

# 方法2 回归计算
df_did['t'] = df_did['treatment'].map(lambda x: 1 if x=='干预后' else 0) # 是否干预后
df_did['g'] = df_did['class'].map(lambda x: 1 if x=='B' else 0) # 是否试验组
df_did['tg'] = df_did['t']*df_did['g'] # 交互项

# 回归
est = smf.ols(formula='sales ~ t + g + tg', data=df_did).fit() 
print(est.summary())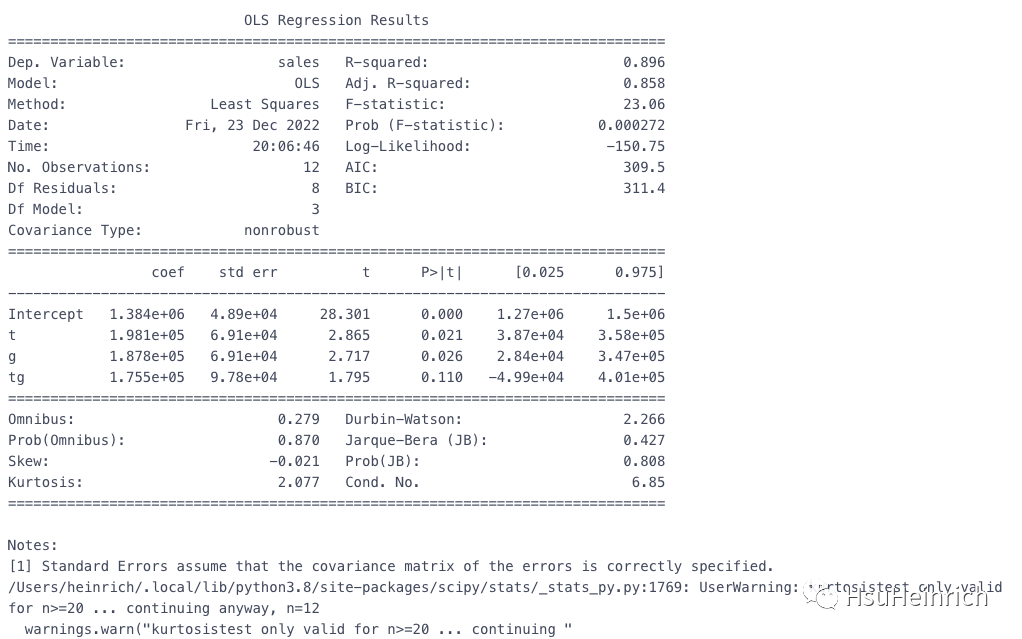

tg的P是0.110，大于0.05，效果不显著，也就是说具备平行趋势，政策没有产生影响。

# 计算因果效应
df_did['treatment'] = df_did['dt'].map(lambda x: '干预后' if x>2007 else '干预前')
df_did_cal = df_did.groupby(['class', 'treatment'])['sales'].mean()
did = (df_did_cal.loc['B', '干预后'] - df_did_cal.loc['B', '干预前']) - \
        (df_did_cal.loc['A', '干预后'] - df_did_cal.loc['A', '干预前'])
print(did)

ch11 Bayes

11.1 ベイズ統計の考え方

• p(A) : 先验概率

• p（A｜B）：后验概率

  • 在得到更新数据之前，参数theta的分布，是分析者主观决定的。
  • 比如选特朗普的概率，抽样100，和抽样1000的概率肯定不一样，但认为认定抽样100的概率就是作为先验概率使用
  • 这是频率学派对贝叶斯学派的主要批判点
  • 作为回应，先验概率通常会设置为标准方差很大，即不管发生什么概率都差不多大的分布。（书上Page 284 的那个图）
  • 但如果知道一部分信息，就可以反映在先验概率里，比如已知选特朗普的人占55%。

• P（B）：证据/数据

• P（B｜A）：似然

• 贝叶斯学派：

  • 贝叶斯学派将概率解释为关于不确定性的一种主观度量。在贝叶斯学派中，参数被视为随机变量，其具有先验概率分布。即随着信息的更新，验证某假说的概率也会随着变化。

  • 对于概率的定义：

    • 关于不确定性的一种主观度量
    • 参数theta随着已知信息的更新而变化

  • 在通过更新信息计算出theta之后，就可以得出概率分布模型，在求模型的面积，就是想求的概率。

    • 书上290页 11.5的公式，就是干这个的。

• 频度学派：

  • 频率学派将概率解释为事件在重复独立试验中发生的频率。在频率学派中，参数被视为固定但未知的常数，因此概率是与频率相关的特性。
  • 对于不确定性的理解：
    • 认为不确定性是在数据抽样的时候不确定性。
    • 这种不确定性可以在固定参数的分布下表达为p（x｜theta）
  • 对于概率的定义：
    • 再进行了无数次的试验后，可以表达客观的频度的值叫概率

情報量基準

KL divergence（To do，神经网络的损失函数常用算法）

• DKL >= 0, 越小代表模型概率分布越拟合真实概率分布。

ベイズ統計の利点

• 推定の結果、統計モデルのparameterを分布として得ることができる。
• ベイズ統計で用いられる計算手法MCMCは乱数を発生させ、Simulationとして事後分布に従うparameterを得るため、複雑なモデリングが可能になる。

11.2 ベイズ統計のAlgorithm（？？？MCMC待研究，我大困惑）

MCMC ？？？？（To do）

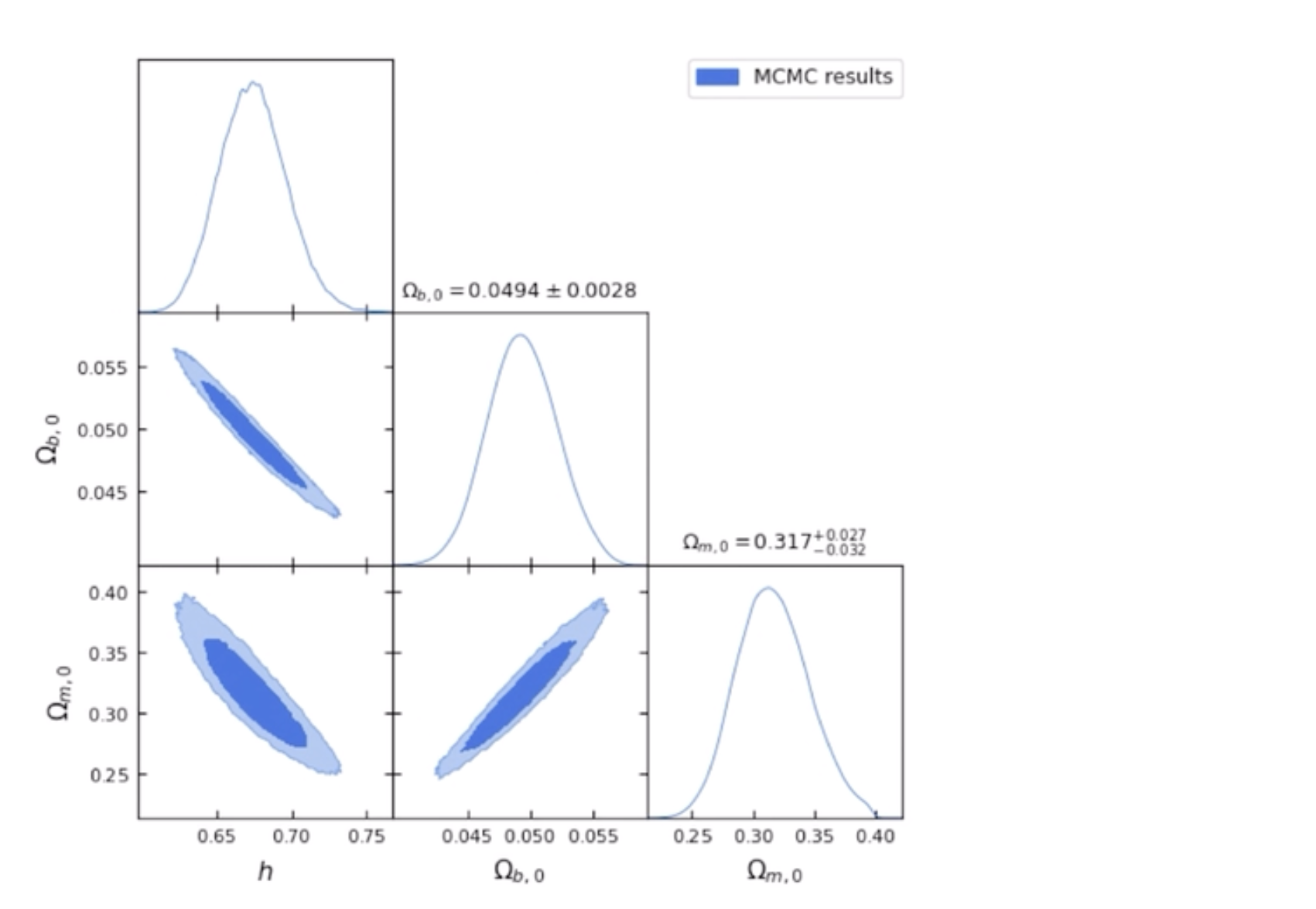
• 图张这样

• 好像一般用于参数限制，待研究

• 乱数を多数発生させて、Simulationし、近似解を得る手法？？？？？

11.3 ベイズ統計の例

二標本の平均値の比較

ch12 統計分析に関するその他の手法

変数の次元

• 変数の数を減らすことを、次元削減（Dimension Reduction）または次元圧縮と呼ぶ
• 高次元データの解釈が困難ので
• 多重共線性を防ぐもできる

Sparse modeling

Principal Component Analysis（PCA主成分分析）

• 主要用于线性分析

• 新しい軸を設定する

• 新しい軸は、データのばらつきが最も大きくなる方向に設定する

• PC1、PC2を呼ぶ

  • 第一主成分
  • 第二主成分

• 寄与率（contribution rate）：各主成分が持つ情報（分散）の割

  • 这些贡献率的和将等于 1，因为它们涵盖了所有方差。通常情况下，我们会根据这些贡献率来选择保留多少个主成分，以保留足够的信息量。

• 累積寄与率：第１から第k主成分までで全体の情報の何％が含まれる

• 主成分負荷量（因子負荷量）（loading）：各主成分の値ともとの各変数の相関変数を計算する

  • 指的是每个原始变量（特征）对于主成分的贡献程度。负荷量表达了主成分中每个原始特征的重要性。
    • 具体来说，一个原始特征的负荷量的绝对值越大，表示该特征在主成分中的重要性越高，对主成分的解释能力也越强。
  • 主成分是原始特征的线性组合，而每个原始特征在主成分中的系数就是该特征的负荷量。
  • 通常情况下，我们可以通过计算主成分与原始特征之间的相关系数来得到负荷量。

• 主成分得点：元の各データを新しい変数を用いて表す。

PCA的数学原理（可以手搓新坐标系）

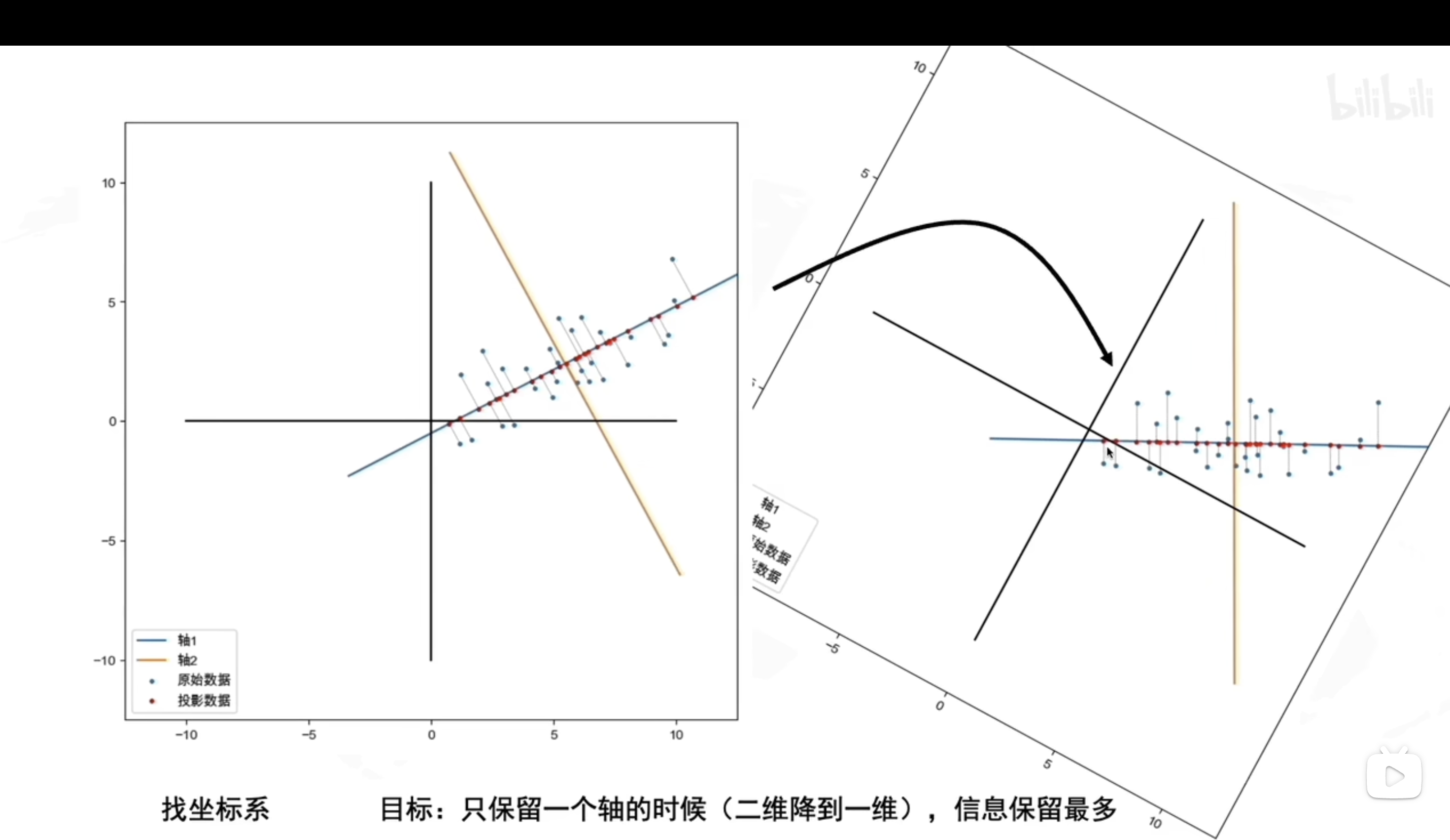
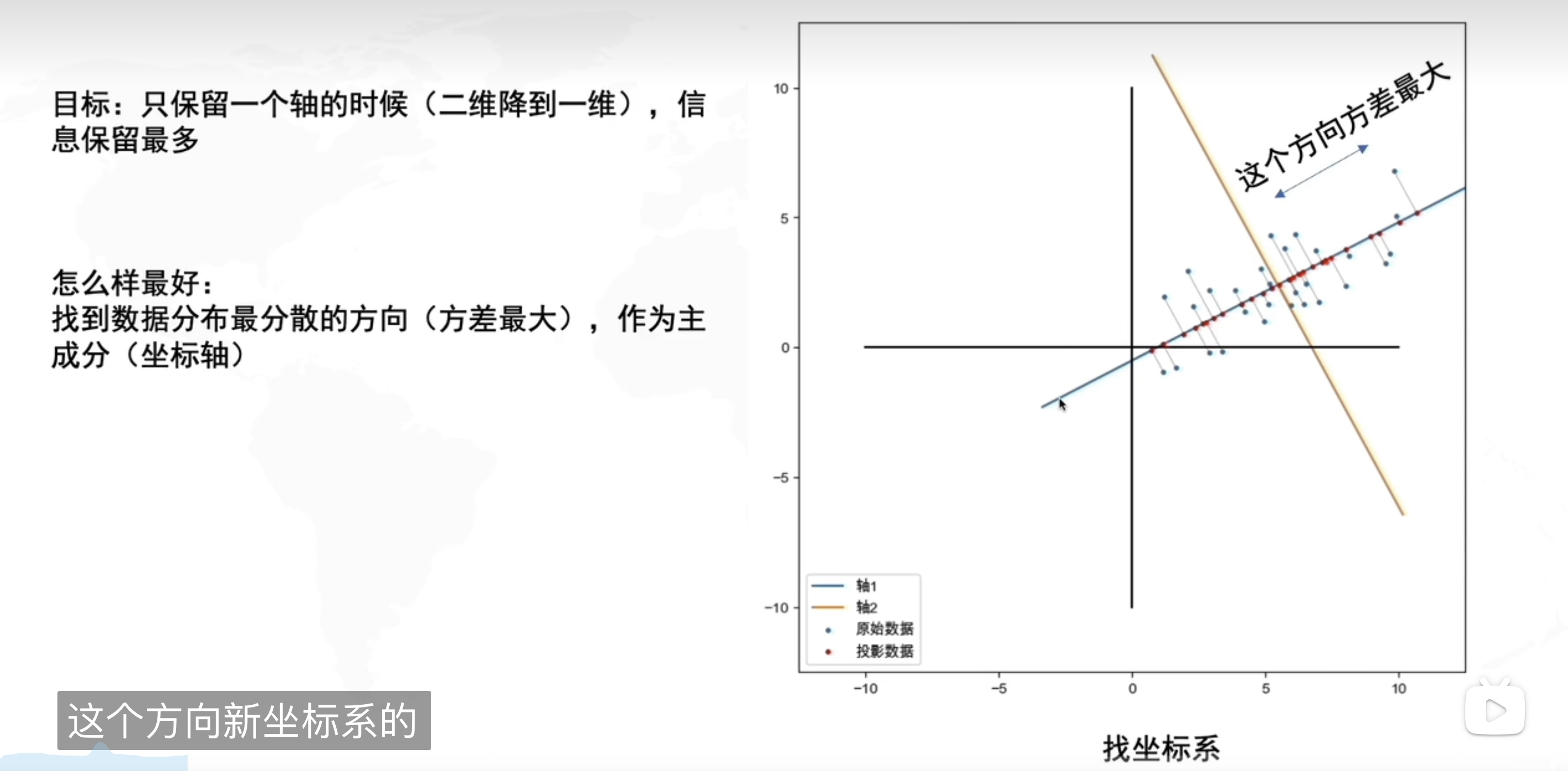
• 那问题不就来了，怎么找到方差最大的方向？

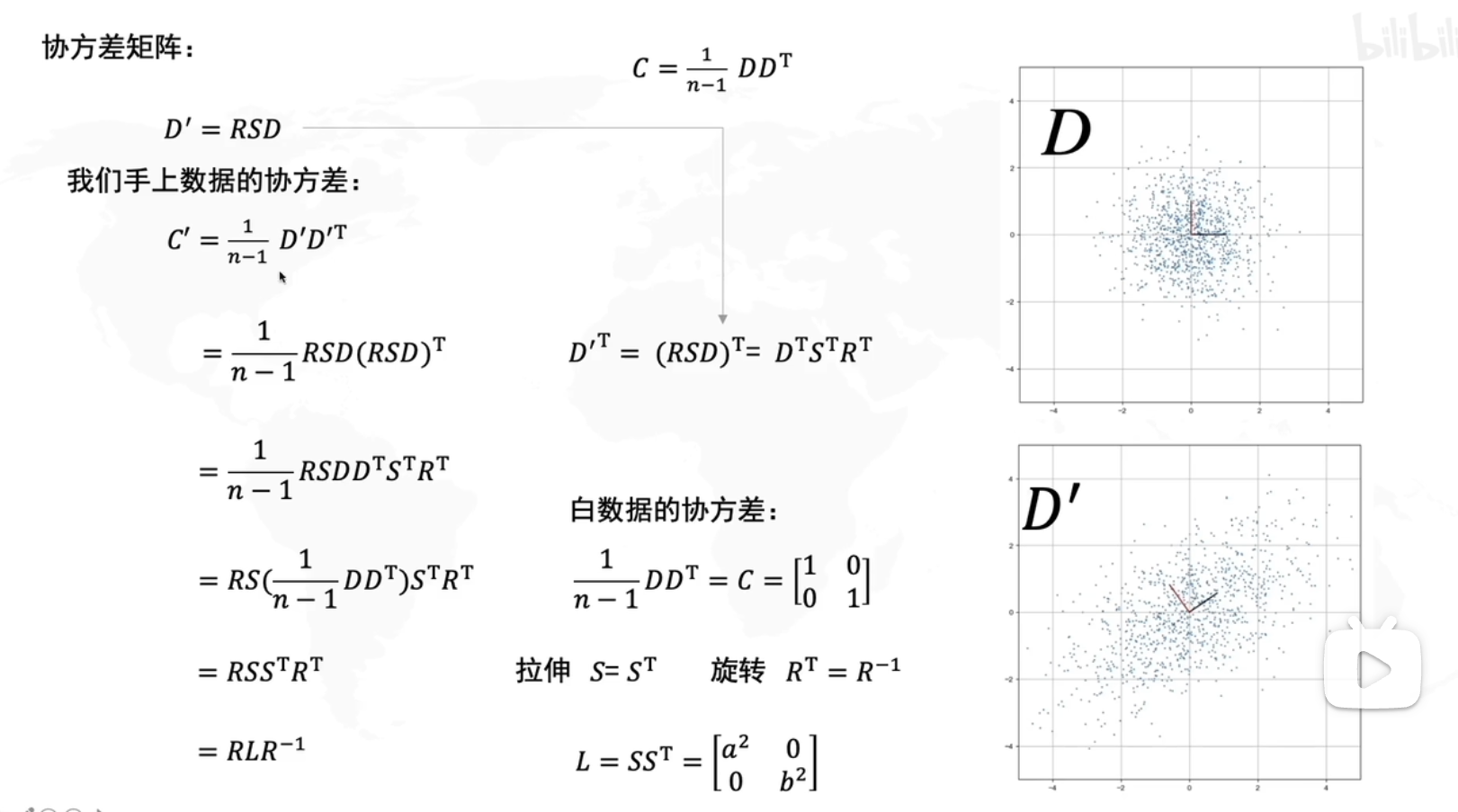
  • 白数据（D）

  • 拉伸（SD）

  • 旋转（RSD）

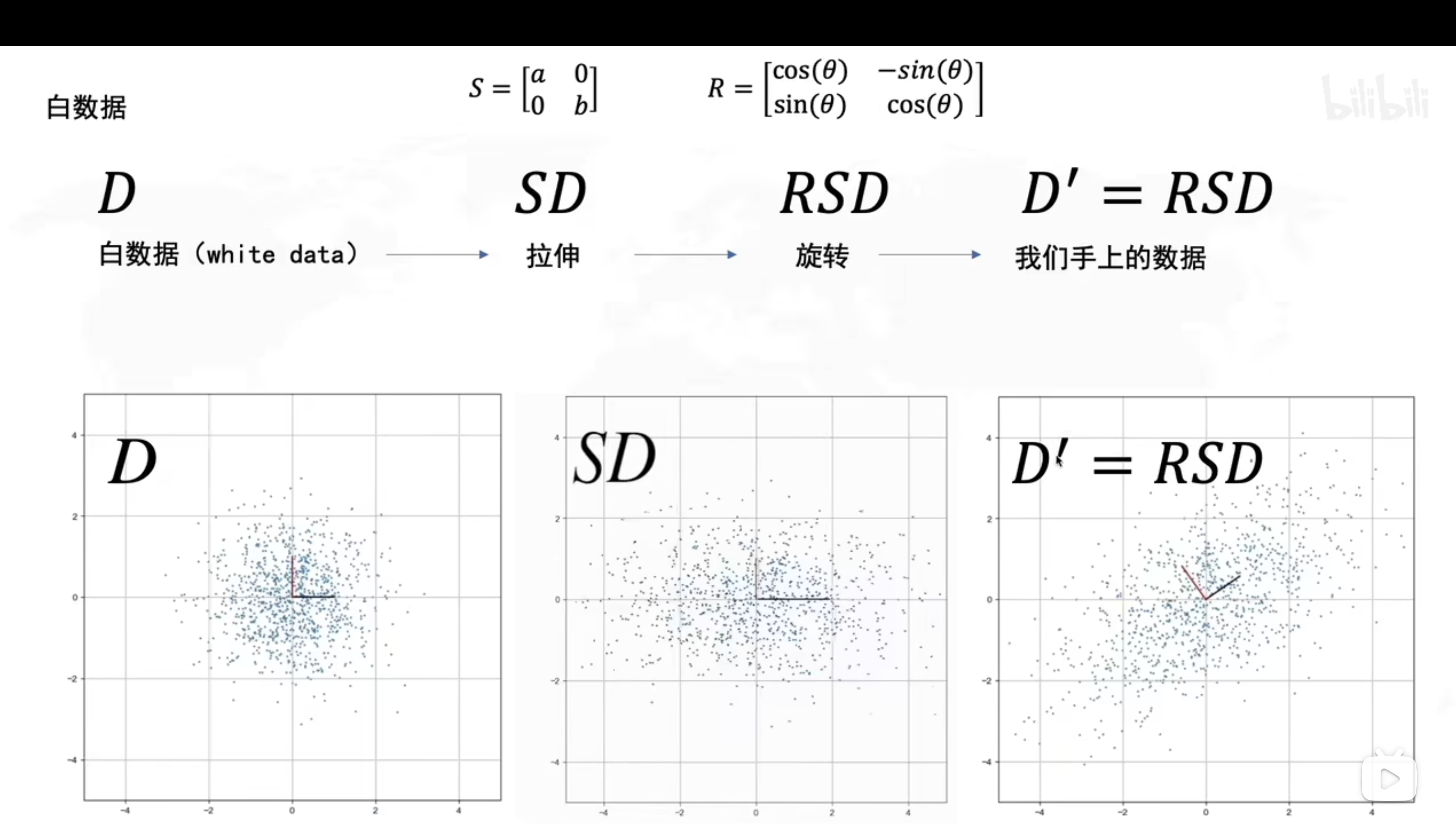
• 也就是说我们要求的旋转角度就是R

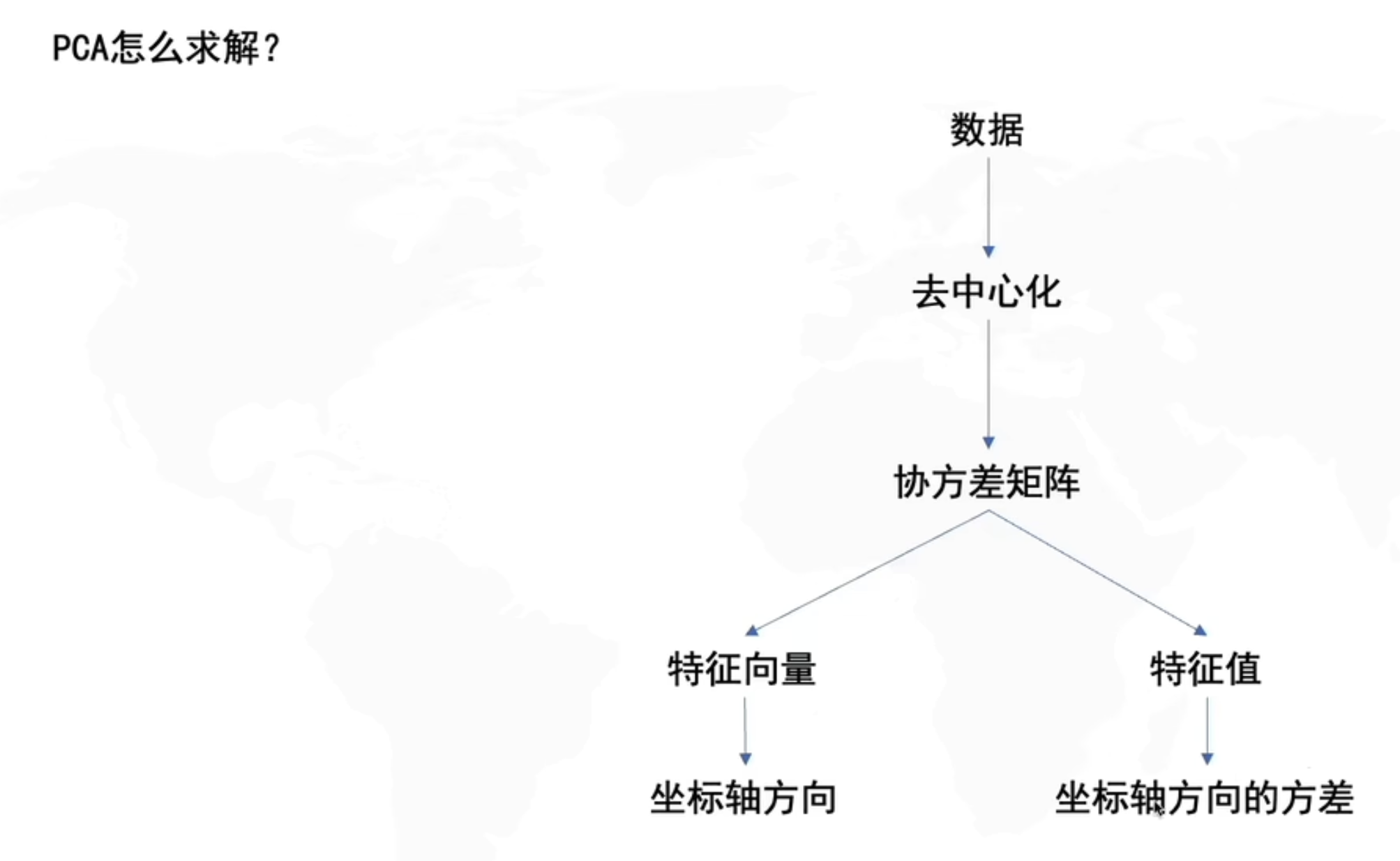
• 求旋转角度的步骤

  1. 求所有数据点的协方差矩阵

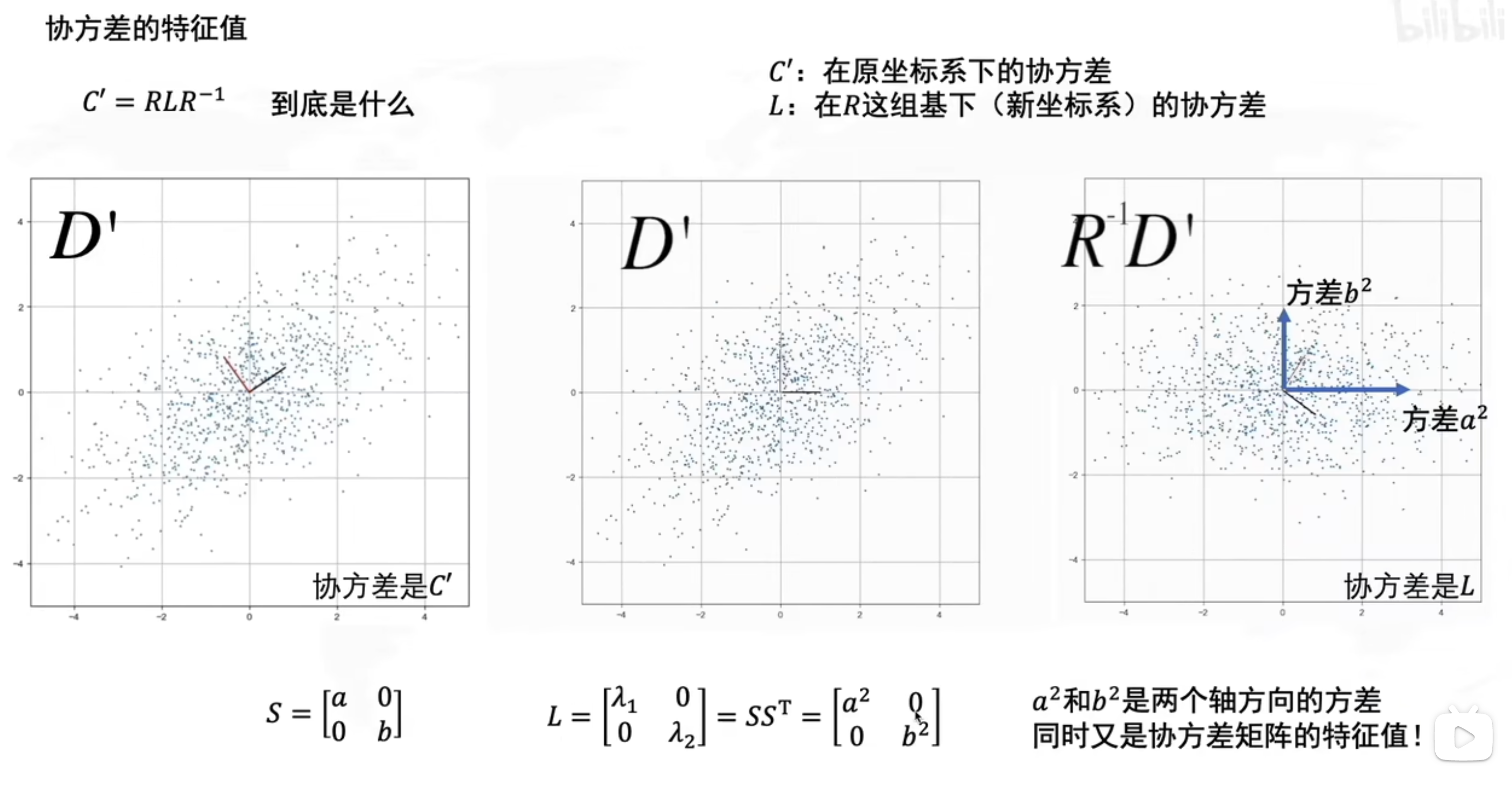
  2. 求协方差矩阵的特征值，特征向量

  3. 求到的特征向量就是新的坐标轴，旋转角度也可以根据求到的特征向量计算

     

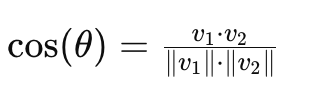
  4. 求到的特征值，就是数据在新的坐标轴上的方差

• 

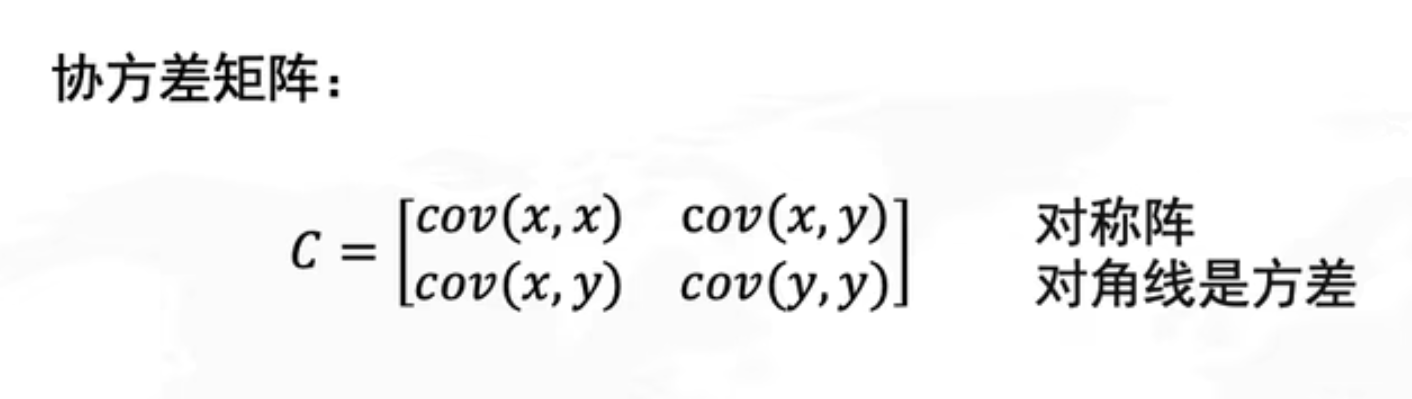
举个栗子

# 举个🌰

假设我们有一个二维数据集，其中包含以下三个数据点：


数据点1：(2,3)
数据点2：(4,5)
数据点3：(6,7)

因子分析

• Pca 是因子分析的一个特例

12.2 Machine Learning

• Data will be used in two situations :
  • Testing the model
  • Training the model

There are three types of meachine learning:

1. Supervised Learning

   • Linear Regression

2. Unsupervised Learning

   • Clustering

     • KMeans

     • hierarchical clustering

3. Reinforcement learning

   • Neural Network

Unsupervised Learning

PCA以外的降维的方法

• t-SNE（可以用于非线性分析）
• UMAP

Supervised Learning

• 分類
• 回帰

Cross Validation

在比较不同模型性能时，为了减少对特定数据集的依赖，并提高模型的泛化能力，需要将数据集分成若干份，然后多次训练模型，每次使用不同的折叠作为验证集，其余部分作为训练集。然后将每次训练得到的模型在验证集上进行评估，最后对所有评估结果进行汇总得到最终的性能指标，从而可以选择效果最好的模型

Confusion Martix

                Predicted Class
              | Positive  | Negative
---------------------------------------
Actual Class  |           |
Positive      |    TP     |    FN
---------------------------------------
              |           |
Negative      |    FP     |    TN
---------------------------------------

在混淆矩阵中，我们将预测的类别与实际类别进行比较。其中：

• TP (True Positive)：预测为正类且实际为正类的样本数量；
• FN (False Negative)：预测为负类但实际为正类的样本数量；
• FP (False Positive)：预测为正类但实际为负类的样本数量；
• TN (True Negative)：预测为负类且实际为负类的样本数量。

通过观察混淆矩阵，我们可以评估分类器在每个类别上的性能，并计算出各种评估指标，如准确率、召回率、精确率和 F1 分数等。

• 当分类器（比如逻辑回归分类器）使用不同的分类阈值时，会得到好多混淆矩阵

• 那能不能把所有的混淆矩阵全都表示在一个二维空间里哪？

• Roc曲线就是干这个用

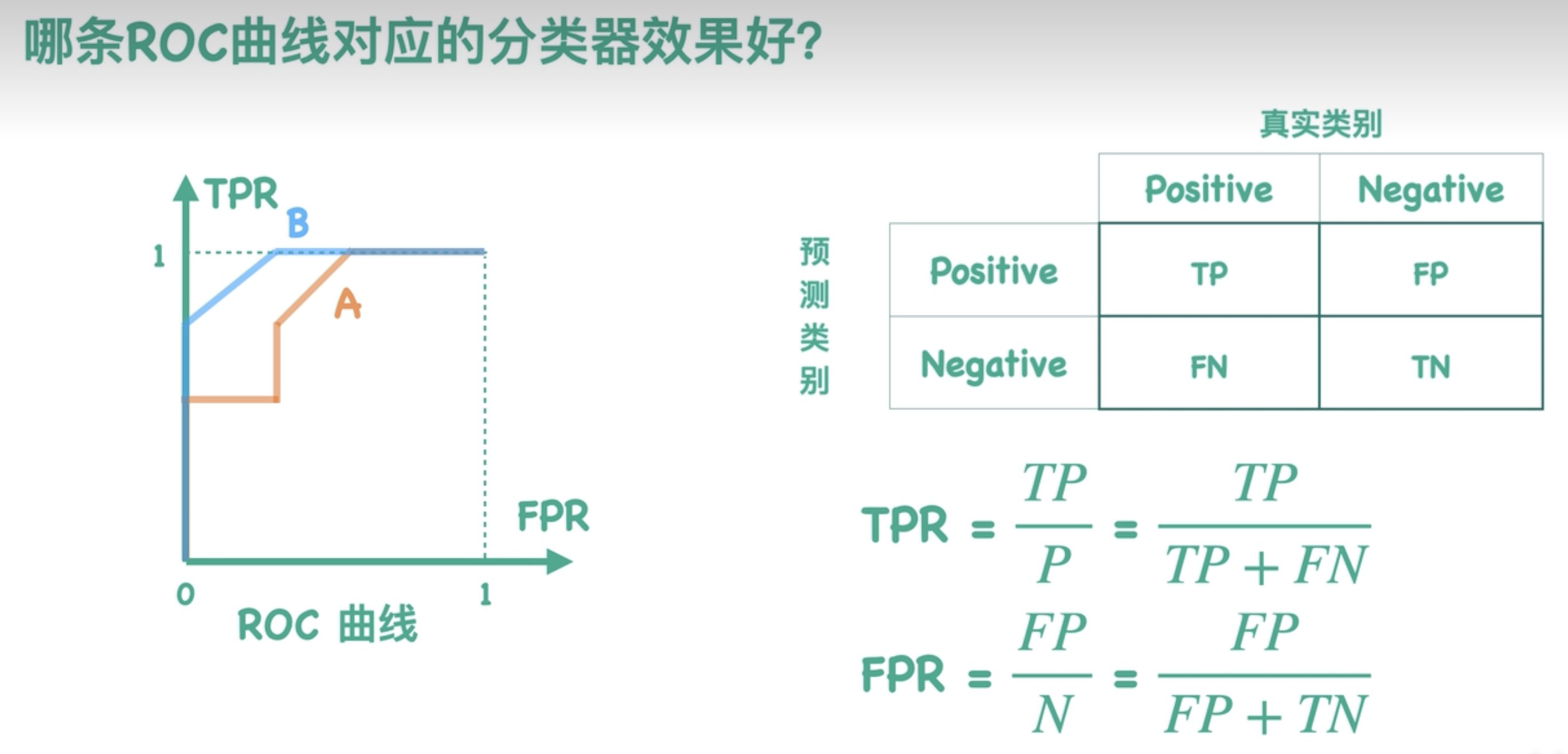
  • 横轴为FPR，纵轴为TPR
  • 阈值越大TPR越小，点越向下移动，最终形成ROC曲线
  • 曲线越靠近左上角越好，因为
    • 同样FPR情况下，TPR越大越好。
    • 同样TPR情况下 ，FPR越小越好。
    • 因此B曲线比A好

• ROC曲线下对应的面积，求出来就是AUC值，用来评估分类器效果的，AUC值一般在0-1之间，越大越好。

ch13 model

• Model:現在のprocessあるいはmechanismを仮定してその挙動を調べる

• 演繹（えんえき）：モデルのparameterをdataから推定し、現実の現象と突き合わせて深く理解する

• モデル化：簡略化によって物事の本質を抜き出すことである。

• 全てを想定しつくつことはできず、現象の真の姿＝真のモデルを手にすることはできないと言える

• しかし、真のモデルでなくとも現象を適切に記述できるモデルであれば、理解に役たち、予測や制御といった目的を達成することができる。

• 数理モデルは二つ種類ある：

  • 決定論的モデル：微分、差分、偏微分など
    • ある時刻での状態が決まったら、次の時刻の状態がただ一つに定まる性質のことである。
  • 確率的モデル：Random Walk、Mrakov過程など

• パラメータを様々に変えたときに何が起こるかを調べることができるのは、数理モデルの強みだと言えます。

• density effect（密度効果）：Parameterが変動したら、確率密度関数も変わる

  • モデルは真実に近くなると、一次導関数微分（First derivative）も０に近く

• 平衡点：一次導関数微分＝０

  • x！＝kになると、この前の状態に戻させると、安定平衡点という
  • x！＝kになると、この前の状態に戻させないと、不安定平衡点という

• 微分方程式の平衡点を調べ、その平衡点が安定か不安定かを調べることで、そのモデルの性質の一端を明らかにすることができる。

• 制御（Control）：就是控制变量

• random walk：就是每次的变化都未知，但试验次数足够多时，遵循中心极限定理就会发现客观规律

• 確率過程：確率的に時間変動する現象を記述する数理モデルである。

• Markov過程：random　walkを一般化した確率過程である。

  • 举个🌰：
  • 一个简单的例子是随机游走。在一维随机游走中，一个物体（比如一只蚂蚁）位于数轴上的某个位置，并以随机步长向左或向右移动。每次移动的方向是根据一定的概率决定的，而与之前的移动方向无关。这个过程就是一个马尔可夫过程，因为在任何给定时刻，物体下一步移动的概率只取决于它当前所处的位置，而不受过去移动路径的影响。

书外逻辑

ANOVA 和 F值

F分布

只有在做Anova（方差分析）时，F值才需要关注

ANOVA（方差分析）

方差分析（ANOVA，Analysis of Variance）是一种统计方法，用于比较两个或更多个组之间的平均值是否存在显著差异。在实践中，方差分析通常用于比较三个或更多个组的平均值是否相等，例如，在不同处理条件下的实验组之间的平均值是否存在显著差异。

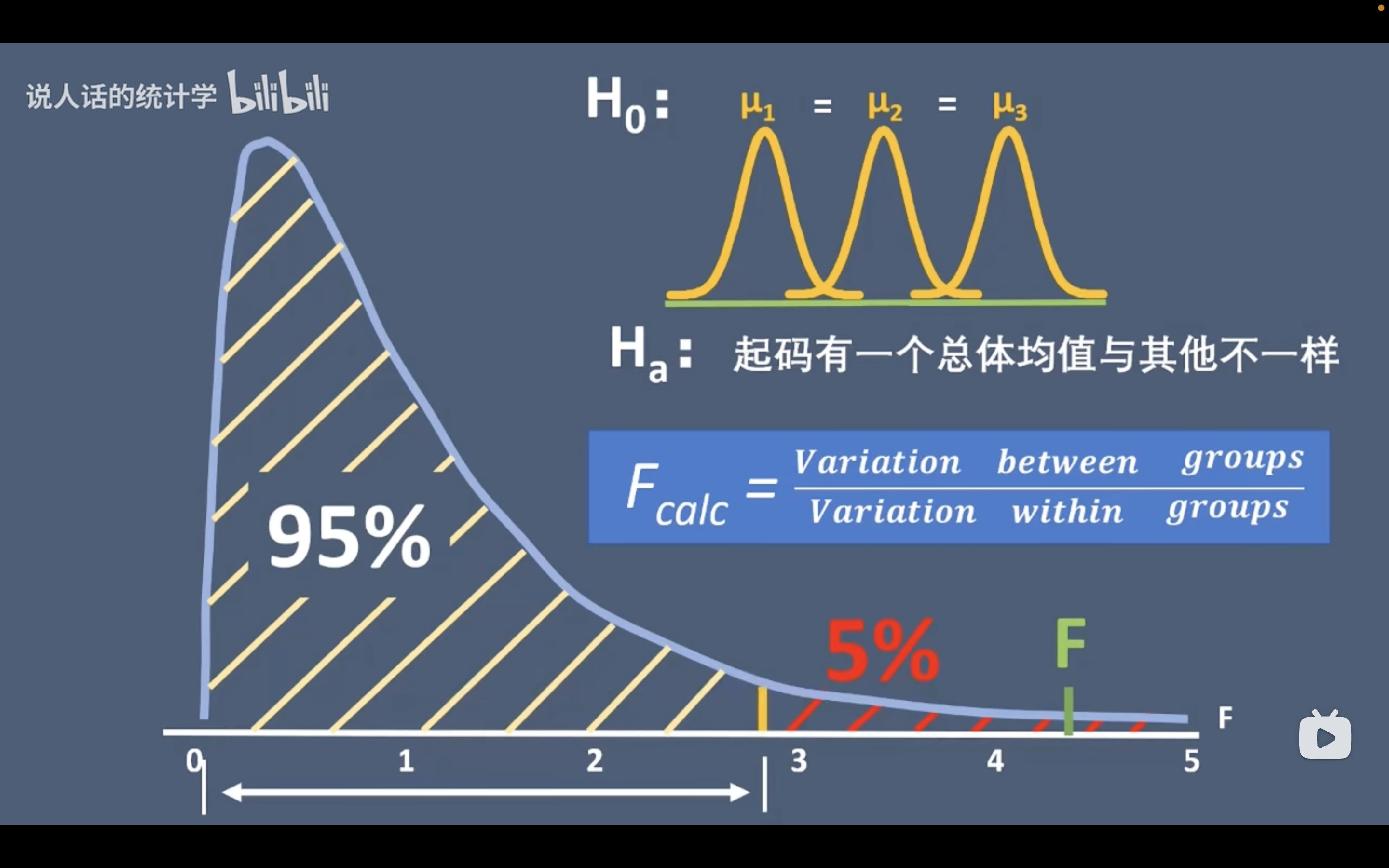
H0：各组总体均值相等

H1:至少有一个总体均值与其他组不一样

F值

F值 = 组间差异 / 组内差异

在方差分析中，F值是用于检验组间变异性与组内变异性之间的比率。具体来说，F值是组间均方与组内均方的比率，其中组间均方是组间平方和除以组间自由度，组内均方是组内平方和除以组内自由度。F值越大，表示组间变异性相对于组内变异性的比率越大，从而说明组间差异越显著。

F值很大，P值小于0.05就可以拒绝原假设

广义线性模型的选择

• y有大致3种情况
  • 连续变量（continuous）：Linear Regression（最小二乘）
  • 有上限的离散变量（binary）：Logistic / Probit Regression
  • 无上限的计数变量（counting）：Possion Regression

p<0.05的新理解

• p 值（p-value）是用来衡量观察到的数据与原假设之间差异的概率。在假设检验中，p 值表示了在原假设为真的情况下，观察到样本数据或更极端数据的概率。

• 更具体地说，p 值是在假设原假设为真的情况下，观察到样本数据或比其更极端数据的概率。如果这个概率很小（通常小于 0.05），我们就会认为观察到的数据与原假设不一致，从而拒绝原假设。

• 简而言之，p 值告诉我们观察到的数据与原假设一致的概率大小，当 p 值很小时，我们倾向于认为观察到的数据并不是由于随机因素而产生的，而是因为真实的效应存在。

• 1-β 表示检验能够正确地发现到真实差异或效应的能力。

• α == 0.05，既是设定的显著性标准，也是第一类错误发生的概率

  • α和β是相反的关系，α变大，β就会变小，反之亦然

  • 所以虽然降低α的标准，可以提高，假设检验的正确性，但同时第二类错误的发生概率也会增加

  • 即H0为假，但接受了H0。（不管H0怎样都接受H0）

  • α 和β，都希望他们越小越好

言葉

Japanese	English・Chinese
要約	summary
発生元	Origin
大まかに	roughly speaking
偏差	deviation
縦軸(たてじく)
扱う	deal with
左右対称（さゆうたいしょう）
偽（にせ）
見なせる	presentable・visible
かいニ乗	Pearson's chi-squared test
適合度検定	检验拟合度
分割表	contingency table 交叉表
表裏一体（ひょうりいったい）
バオーとレット検定	Bartlett test
シャピロ ウイルク検定	Shapiro-Wilk
当てはめる	Apply
影（かげ）	Shadow
共変量	covariate
衰える（おとろえる）	aging（Due to aging）
むやみや	recklessly
制御	propensity （for violence）
	Control