ch1 データを観測する

• 測りにくいものを定量化する際、「測りやすい」指標が優先的に使われやすい傾向がある
• 何かのOutputを測りたい時に、測りやすいInputに関する量で代替させるおいう誤りは、色々ある。
• データの量と扱える情報の細かさには　trade off　が存在する。
  • 細かいデータ：一部の状況しかわからない
  • 大量のデータ：標準化が必要、全体の傾向がわかる

ch2 誤差とばらつき

2.1 誤差の分解

• 誤差：観測された値と真の値の差である。
• 観測値に含まれる誤差が、検出したい値の変化の大きさよりも大きい場合、その観測値だけから直接なにかを結論つけることができなくなる。
• データをたくさん集めて誤差の特性を評価することで、ある程度の推論が可能である。
• （ランダムご誤差）Random error：偶然誤差
• （バイアス）Bias：系統誤差
  • バイアスだけ大きい場合、観測値を信用できない

2.2 誤差と確率分布

• 確率分布：どの値がどれぐらい頻度として観測されやすいかを表現したものである。
• 確率分布が存在する前提：
  • 実際のデータはその確率分布から確率的に得られたと考える。
• 確率変数：ランダムに得られる値を取る変数

2.3 [確率分布に関するまとめ]

• 分散
• 平均
• 標準誤差
• 確率分布：データの値ごとにそれが得られる確率を全ての場合について記述した
• 離散値
• 連続値：取り得る値が飛び飛びでない
• 確率密度関数：
  • 離散変数の場合：それぞれのビンを一番細かく設定すれば、この時点でこれが確率分布となる
  • 連続変数の場合：最終的にはビンの幅は無限に小さくなり、それぞれのビンの高さを繋ぐと関数が得られる。
  • 確率密度関数：その領域の面積が求めたい確率に対応する。面積が確率に対応するので、確率密度関数を全ての領域にわたって積分すると、必ず１になる。
• 正規分布（Gaussian Distribution）
  • 特徴：極端に大きい値が「ほぼ出ない」
• 中心極限定理：確率変数の値を足し算していくと、その和の確率分布は正規分布に近づいていきます。つまり、様々なランダムな要素が足し合わされるような状況では、自然と正規分布が出てくる。
• 得られたデータからhistgramを描く、このように得られた頻度分布、確率分布のことを、経験分布という。
• 一方で、正規分布のように、数学的な仮定から計算される分布のことを、理論分布という。

ch3 データに含まれるバイアス

3.1 測定基準に関するバイアス

• 分析対象のデータが一貫して基準によって測定されていないこともある。

• 他人の手によってまとめられたデータでは、非常に見逃しやすい

  • だから、測定基準を確認することを習慣つける。

• 「測られているもの」が、「測りたいもの」と乖離して時間的に変化していくこともある。

• 測定されているものじたいは同じでも、その数値が意味する内容は時々刻々と変化することはよくある。もし適切な補正が可能である場合は、それを行なってから分析を実施する。

3.2 選択バイアス

• 選択バイアス：全体から見て、一部のデータが選択されたことに起因する
• 生存者バイアス：生き残ったものしか観測されないバイアスである。
• Sampling Bias：Samplingによって、データの偏りが生じる。
• 志願者バイアス（Volunteer Bias）：実験参加に対する意欲が高い、あるいは実験内容に何らかの関心がある、これも偏ったsampleになってしまう
• データ観測時によってほど気を使わない限り、常にデータは何らかの意味で偏ってしまうと考えておくのが良いである。

3.2　たまたま報告されている時

• たまたま報告されている時
  • 仮説に合った結果が得られなかった場合には、その結果は報告されないということです。
  • 逆に仮説が間違っていても、Samplingの問題やデータのrandom誤差のせいで、「たまたま」仮説に合う結果が出てしまった場合、それは報告されてしまいます。

3.3 観測介入に起因するバイアス

• 測定や実験を行うこと自体が対象に影響を与えてしまうためである。

• 信用できない回答

  • 質問に回答する個人が後ろめたいと思っている事柄については、正確なデータが得られないこともある。

• 無意識的な要因に自身の選択が影響されるだけでなく、自分が行なった行動に対して簡単に誤った理由付けをしてしまう

3.4 データの扱いに起因するバイアス

• データを扱う人が意図的または無意識的にデータを歪む
• 目標が決められていて、本人の裁量で簡単に（望ましい方向に）コントロールできる数値については、こうした不正によってデータが不正確になることもある。
• 確証バイアス：自分の仮説や信念に整合する情報ばかり集め、それらに矛盾する情報を無視または集めようとしない傾向がある。

ch4 交絡因子と因果関係

4.1 二つの変数の間の関係

• 相関関係

  • 相関係数：

    • 相関係数が正の値であるとき，片方の変数が大きくなればもう片方も大きくなることを意味し、二つの変数には「正の関係がある」という
    • 逆に、相関係数が負の値であるときには、片方が大きくなればもう片方は小さくなることを意味し、「負の関係がある」という

  • 相関の絶対値が大き時には、それらの変数の間に何らかの関係があることを示すヒントになることがよくある。

• 因果関係：

  • ある事象が別の事象に影響を与えているとき、二つの事象の間には「因果関係がある」という
  • データだけから、このような因果関係を結論つけるは、しばしば非常に難しいです。

• 相関と因果関係

  • 変数の間に強い因果関係がある場合、一般にそれは変数間の相関として現れる。
  • しかし、逆に相関があったとしても、それは因果関係を意味しない。

• 変数間の関係性まとめ

  • 因果関係はそのものは存在するのは、この介入（武器軟膏を用いる・用いない）によって結果の変数（治りやすさ）に影響を与えることができる。
  • 二つの変数の間に強い相関がある場合、片方の変数の値が分かれば、もう片方の変数も同じように変化しているはずなので、それを利用して値を予測することができる。目的が予測することだけであれば、必ずしも因果関係を特定しなくてもいいである。
  • 介入による結果の操作や相関を使った予測を行うことを含めて何もできない。しかし、見せかけの関係性に騙されて、こうした主張を行ってしまうケースは現実によくある。

4.2 交絡に対処する

• 交絡因子：原因となる変数と関連し、かつ結果の変数と因果関係を持つ要因のことである。

  • 通訳：指与原因变量相关并且与结果变量具有因果关系的因素

• 因果関係推論の根本問題：

  • 介入を行ってしまうと、その介入を行わなかった場合のデータを取得することができなくなってしまう。

• RCT実験（ランダム化比較実験）（Random Control Test）：

  • この方法では、集団を対象として分析を行い、着目する変数の平均的な効果（平均処置効果：average treatment effect）を評価することを目指す。
  • データはランダムに二つのGroupを分ける：
    • 処置群（実験群）
    • 対照群（統制群）

• 観察データと実験データ：

  • 観察データ：

    • 被験者を集めて実際に介入を行って得たデータを、実験データをいう。

  • 実験データは取得のコストが大きい反面、着目していない要因によって結果が影響されにくいように、事前にデータの取り方をコントロールしやすいという利点がある

  • 観察データを用いた研究「観察研究という」では、交絡因子を十分にコントロールすることが一般に難しく、注意が必要ある。

4.3 ランダム化比較試験ができないとき

• 重回帰分析：

  • 定義：目的の変数を着目する変数の足し算で表現することで、それぞれの要因がどれぐらい影響を与えているかを評価する方法である。
  • これらの変数に係数を掛け算して足し合せたものを用意し、その係数を調整することで目的となる変数の値を再現する。
  • 利点：目的変数に影響を与えていると思われる変数が全てデータに含まれていれば、それぞれの影響を個別に評価できることである。つまり、交絡因子の影響を差し引いた上で着目する変数の影響を評価できる。
  • 弱点：この分析でわかることは、相関関係だけなので、必ずしも直接の因果関係の存在や方向を特定できないことが挙げられる。
  • 重回帰分析には、単純な足し算だけではなく、要素同士の掛け算も式にも含めることができる。
  • 交互作用：組み合わせによって生じる効果を表現することができる。

• Logistic回帰：

  • ダミー変数：元々数字でない事象を数字に置き換えたものである。

• 回帰不連続デザイン：実験設計の一種で、被験者や観察単位をいくつかのグループに分割し、各グループに異なる処置（または条件）を与えることで、処置の効果を評価する手法です。

• 傾向スコアマッチング：

  • バイアスを避けるために用いた手法である
  • 複数の交絡因子をひとまめにした総合得点のようなものである

• バランス化：交絡因子となる要因について、二つの群で全体として一致するように調節することである。

• ランダム化比較試験が行える場合、それを実施するのはベストである。

ch5　Data Sampling の方法論

5.1 Sampling の考え方

• Sampling調査：対象となる集団の一部だけからデータを観測し、そこから全体の性質に関する推論を行うことができる。
• 標本：取り出した一部のデータのこと
• Sample Size:標本に含まれている観測値の数のこと、nである
• サンプル数：標本が何のセットがあること
• 無作為抽出：ランダムにサンプリングを行うこと
• 標準誤差：標本平均のばらつき
• 信頼空間：この範囲を、「結果かその中に収まっていれば、十分結論を出すことが出来る」と言うところまでサンプルサイズを増やすことで

5.2 様々Sampling法

• 無作為抽出方法：

  • 単純無作為抽出：すべてのデータを用意し、そこから乱数によってサンプリングしていく方法
  • 系統抽出：乱数を使わずに、データリストの上から一定間隔でサンプリングしていく方法。
  • 層化多段抽出法：個々の対象が所属するdata blockでランダムに選択することで、対象を絞っていく方法
  • クラスター抽出：対象が何らかのクラスターを形成している場合、それを利用してクラスターことに要素を抽出する方法

• 無作為でない抽出法：

  • 有意抽出：「母集団を代表していると思われる対象たち」を主観的に選んでデータを取得方法
  • 便宜的抽出：「データを取りやすい対象を調査する」方法である
  • サンプルリングバイアスが生じうる方法で標本抽出を行った際に重要となるのは、「その標本において得られた結果が、母集団全体でも同じように成り立っているか」ということである。

5.3 Sampling & Bias

• 標本抽出枠（Sampling frame）：標本を選ぶために使用するリストのこと
• Coverage error：標本抽出枠に含まれていない要素があると、誤差の元となる。
• dualーframe：2つの異なる抽出フレームを用いてSampling

ch6 データの扱い

6.1 取得したデータの確認

• データを入手した側の人は、「データを基本的に、正しく取得・処理されたものである」という想定で分析を行ってしまいがちです。しかし、実際に人々が手にするデータには、無視できない割合で何らかの間違いが含まれている。

• そのようなデータを分析、解釈した結果を論文として発表したり、それに基づいて大きな意思決定を行なってしまうと、しばしば重大な損害が生じる。

• データに含まれる誤りはしっかりと見つけ出して対処する必要があるし、また、自分が収集・処理したデータを外に出すときには、絶対に間違いがあってはない。

• そもそも、データを手で入力しなければならない状況が一切発生しないようにすることは重要である。データは、手で触れば触るほどエラーが載るという風に考える。

• どの値からどの値が計算されているのか一度きちんと追跡してチェックする。

• 異常値：データ取得の時点で起きた何らかのミスや、計測器の異常などによって発生する外れ値を異常値という。

• 外れ値に大きく左右されないような分析手法を選択肢するなどの配慮を行う必要がある。

• 複数の変数の値をまとめて見ることによってしか見つからない外れ値もある。

• 多くの場所で値が厳密に０（あるいはNanなどの別の値）になってしまっている。

• 「値が他の観測値と比較して特に大きい（小さい）が、本当にそういう値だった」といったパターンもあり得るからである。

• 一見して異常値が見える値が観測されても、実際に分析から除くべきかどうかは、しばしば難しい問題である。

• 逆にそのような理由がない場合は、単に他の観測値から離れているからといって安易に除いてしまってはいけない。

6.2 データの分析操作

• データ分析においては、この前処理に一番時間がかかるといっても過言ではない

• 一つ一つ処理の前後で、想定あれる処理が正しく行われていることを逐一すべて確認する。

• 逆にやってはいけないのは、複数の処理をまとめた分析を最初から行ってしまうことである。

  • 特に、二つ以上のエラーが同時に発生してしまうと、発生しうるエラーのバターンが掛け算で増えるので、かなり分析に熟練人でも特定に時間がかかてしまうである。

• 同じ処理を行うコードは一つにまとめることは大切である。

• 同じ処理を行うコードは一か所にまとめ、安易にコピーして使わないことも大切である。

• 分析コードを修正してアップデートする場合は、必ず日付と、どのような修正を行ったのかを記録しておく。

• 分析コードは、そこから出力された結果については、両者の対応がつくように名前をつけて管理することも大切である。

• ソフトウェアを使用した分析においても、どのデータに対してどのような処理を行なったのかについて記録して管理しておく。

• 処理コードや処理後のデータは往々にして、後からどのような処理を行なったのが確認するために参照されることになる。

• そもそもこれらの分析プログラムに間違いがないか

• 設定・計算されたものが、期待したものと違った、おいうケースはよくある。

6.3 データの保管・管理

• データ分析の元となったデータや資料は、何らかの不備が見つかった後でも検められるよう、管理しておかねばなりません
• データ分析の結果を学術論文に発表した場合、そのデータは原則10年間保存することが望ましい。
• データ取得を計画する階段で、データを誰が、いつまで、どのように保管するのかについて検討しておくことは大切である。
• 外部からの攻撃に対する保存媒体の脆弱性の問題よりも、内部の人間による人的な要因によるものがほとんどである。
• 個人情報の取得、保管、譲渡、開示などの取り扱いについては、法律に従う。
• そもそも不必要な個人情報は取得しないようにする。
• 複数の個人データを統計処理したものは、原則として個人情報には当たりません。
• データの取得・分析だけでなく、入手したデータをどのように管理・運用するのかについても、しっかりと計画しておく。

ch7 一変数データの振り舞い

7.1 記述統計量を考える

• 量的変数

• 質的変数

• カテゴリ変数

• 記述統計量・要約統計量

  • 中央値：データの真ん中周辺の様子を表す

  • 平均値：全体の振る舞いを特徴づける量です

  • 最頻値：最も多く表す値の様子を代表する。

  • 最大値

  • 最小値

  • percentile

    • 第一四分位数
    • 第二四分位数
    • 第三四分位数

  • 箱ひげ図（boxplot）

    • IQR
    • 

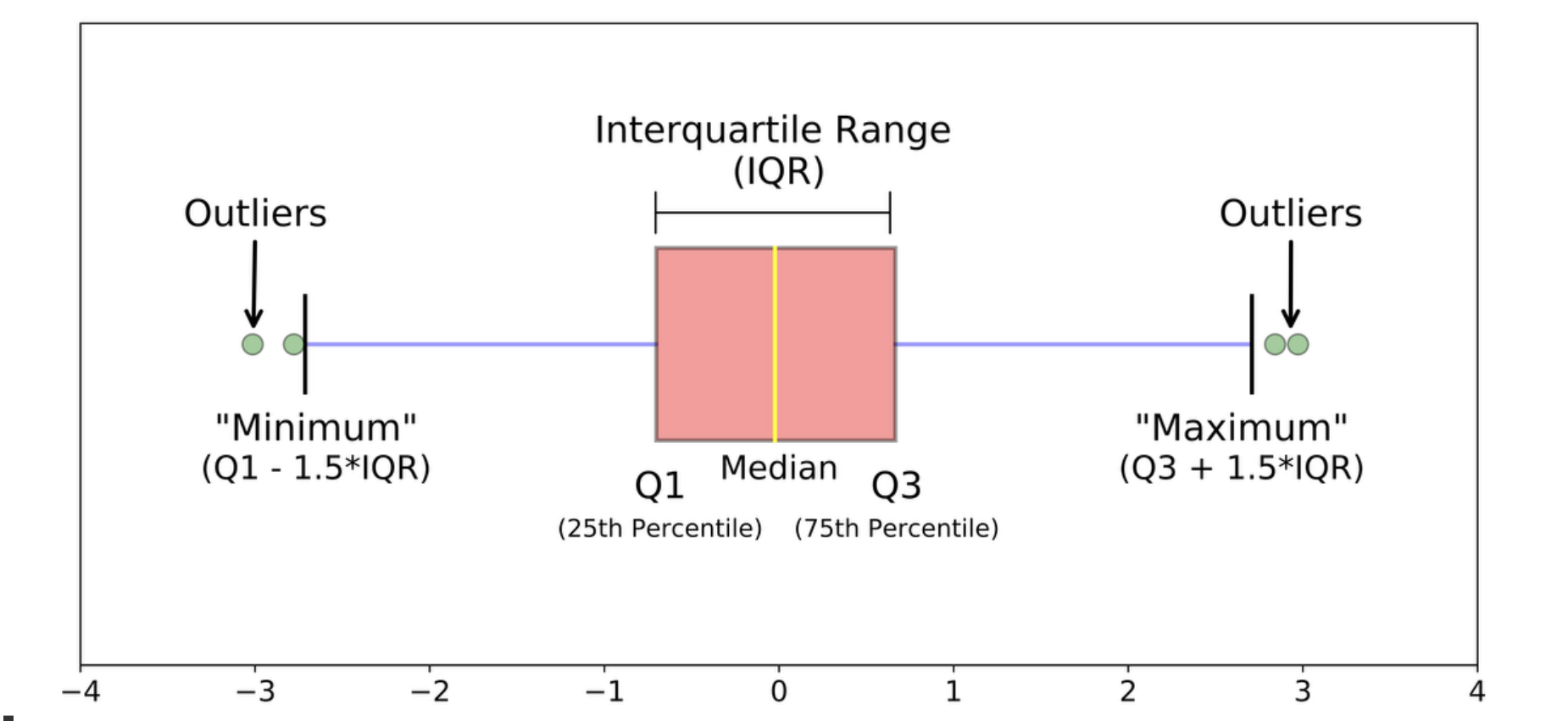
• ばらつきを捉える記述量

  • 平均
  • 分散

7.2 データの分布を考える

• strip plot

• Swarm plot

  • 

• error bar

  • 

• Violin plot

理論分布と対応つける

• 対数の正規分布

  • 非常に大きい値が発生しやすいとき対数正規をとる。
    • 就还是压缩数据，只不过以不同的方式而已，和z-score之类的原理是一样的
  • 裾が厚い分布
    • 裾が厚い分布には、しばしば分散や平均値が存在しないことがあり

• 累積分布関数

  • 関数の左の面積をみったら、データの割合がわかる
  • 関数の変動speedをみったら、データはどのような分布があるかとわかる
    • 例えば、変動speed急に大きくなると、データはここでの分布が多いである。
  • この関数は、xのbinは設置いらない。

• 時系列のデータは取り除きたい

• 周期変動

• 最も簡単な周期変動の取り除き方として、周期ごとに差分をとるである

• 自己相関（autocorrelation）：「過去の値がどれくらい未来の値に影響を与えているか」を定量化方法

ch8 変数の間の関係を検める

8.1　二つの量を比べる

• 二つの量を比較するときには、データで見られた差がばらつきの範囲と比較して十分に大きいのかということは調べなければならない。

  • その差は何回計算しないとは説得力がない

• 観測値の差がばらつきと比較して、ばらつきの大きさが明らかに小さいなると、単に1回の観測値同士を比較して結論を導いてはいける。

• 比較基準として、一般的に：

  • １倍標準差
  • ２倍標準差
  • 3倍標準差
  • 

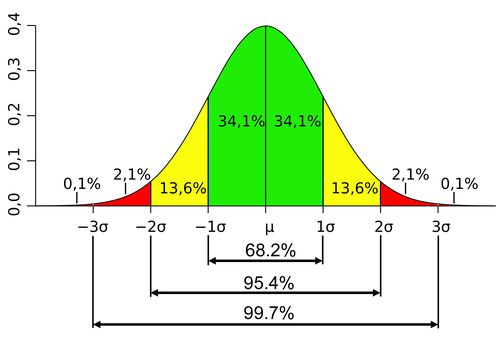
• 仮説検定：データからの性質、たまたまであるかと知りたいときに、仮説を作って、検証できる

  • H0：帰無仮説

    • たまたま

  • H1：対立仮説

    • 検証したい性質
    • たまたまではない

• p-value：在H0为真的情况下，观察到的数据发生极端情况的概率。

• 求的p<0.05的话，走H0，偶然数据，验证的东西说明不了

• 反之走H1，拒绝原假设

• 有意水準alpha：H0にか？H1にか？の基準

• 正規性：データ分布は正規分布かどうか

• U检验：用于比较两个独立样本之间的中位数差异

  • 当数据不符合正态分布的要求时。
  • 当样本容量较小，无法使用z检验或t检验时。
  • 当研究者关心的是中位数而不是均值的差异时。

• F-Test:

• T-test：

  • 适用于样本容量较小（通常小于30）的情况。

  • 当总体标准差未知时，且样本服从正态分布或接近正态分布时，通常使用t检验。

  • 主要用于方差相同时比较两个样本均值是否有显著差异（students‘s T test）。

  • t valueはH1に落ちったら、dataがT 分布に従う

    • T value から　P valueを計算できる、式は、in file named '各种数学'
    • t valueは二つの群の差を定量化した量である。

  • 举个🌰

  • 最常用的是检验一个正态分布的参数μ和σ是否正确

    • 在统计中抽样的结果不只是正态分布（U函数），它只是最常见的一种
    • 还有其他分布，比如t分布（T函数）
    • 可以使用标准化的t函数，反过来检验正态分布的参数是否正确
    • 举个例子，把已知的正态分布的参数，带入t函数得到落在x轴上的值
    • 如果落在拒绝域内，则参数错误

• 対応がある比較：二つのグループの間で観測値同士を紐付けて比較すること（p１５０図）

• 対応がない比較：紐付けない

8.2 二つの量の相関を調べる

• 相関を調べるときに、一つの観測値対象から二つの情報を取る必要がある

• まず、データを散布図にplotし、相関係数を計算する

• 二つの変数の間いに大きな相関が認められる場合、何らかの関係性があることが示唆されたことになるから、それを足掛かりにして、より詳しい分析を進める。

• 絶対値の大きい相関係数の値、つより相関関係がある。

• 相関係数について注意点；

  • 相関係数は外れ値に極めて大きい影響されるので注意しなきゃ
  • データの中に複数のグループが存在しているときにも注意しなきゃ

• 数据相关和相关系数大是充分不必要关系

  • 数据量小的时候经常出现相关系数大，但不相关的情况

• 無相関検定：

  • H0：相関性ない
  • H1：相関性ある

ch9 多変量データを解釈する

9.1 探測的分析と多重検定

• 探測的データ分析：データから特徴を見つけ出すための分析である。

• 確証的データ分析：検証したい仮説がある分析。

• 検定の多重性：仮設検定が何度も繰り返すことで発生する問題

  • 探測的に相関をいろいろ調べておくと、本来は関係がない変数の間にも相関が見えてしまうことがよくある

• 多重性を補足する：

  • Bonferroni法：検定の回数をM回として、有意水準をMで割ったものを採用する。

  • 問題：

    • 做多次检验时，M很大，一除，p想比他小都很难，容易不准
    • 容易发生第二类错误

  • Holm法：

    • 第一个设置的显著性水平：p/M
    • 第二个设置的显著性水平：p/M-1

• 探索的データ分析で見つかったデータの特徴が「たまたm」見つかったものではないかどうかは、仮設検定ではうまく評価できないのである。

• 発見した特徴が「たまたま」生じたものでないことを疑う必要がないほど、サンプルサイズの大きさなデータを入手できている場合には、そもそも仮設検定を実施する必要がなく、このような問題は発生しません

  • 如果拥有足够大的样本数据，不必怀疑所发现的特征是否仅仅是“偶然”出现的，可能根本不需要进行假设检验，也就不会出现这种问题。

9.2　分散分析と多重比較

• 分散分析（ANOVA）：方差分析（Analysis of Variance，简称ANOVA）主要用于比较多个样本均值之间的差异，以确定这些样本是否来自相同的总体。方差分析使用F分布

  • F分布：

    • H0:通常假设两个或多个样本的方差相等。即各样本组之间没有差异
    • H1**:至少**有一组方差和其他组不相同。即各样本组之间至少有一组和其他组存在差异。
    • 

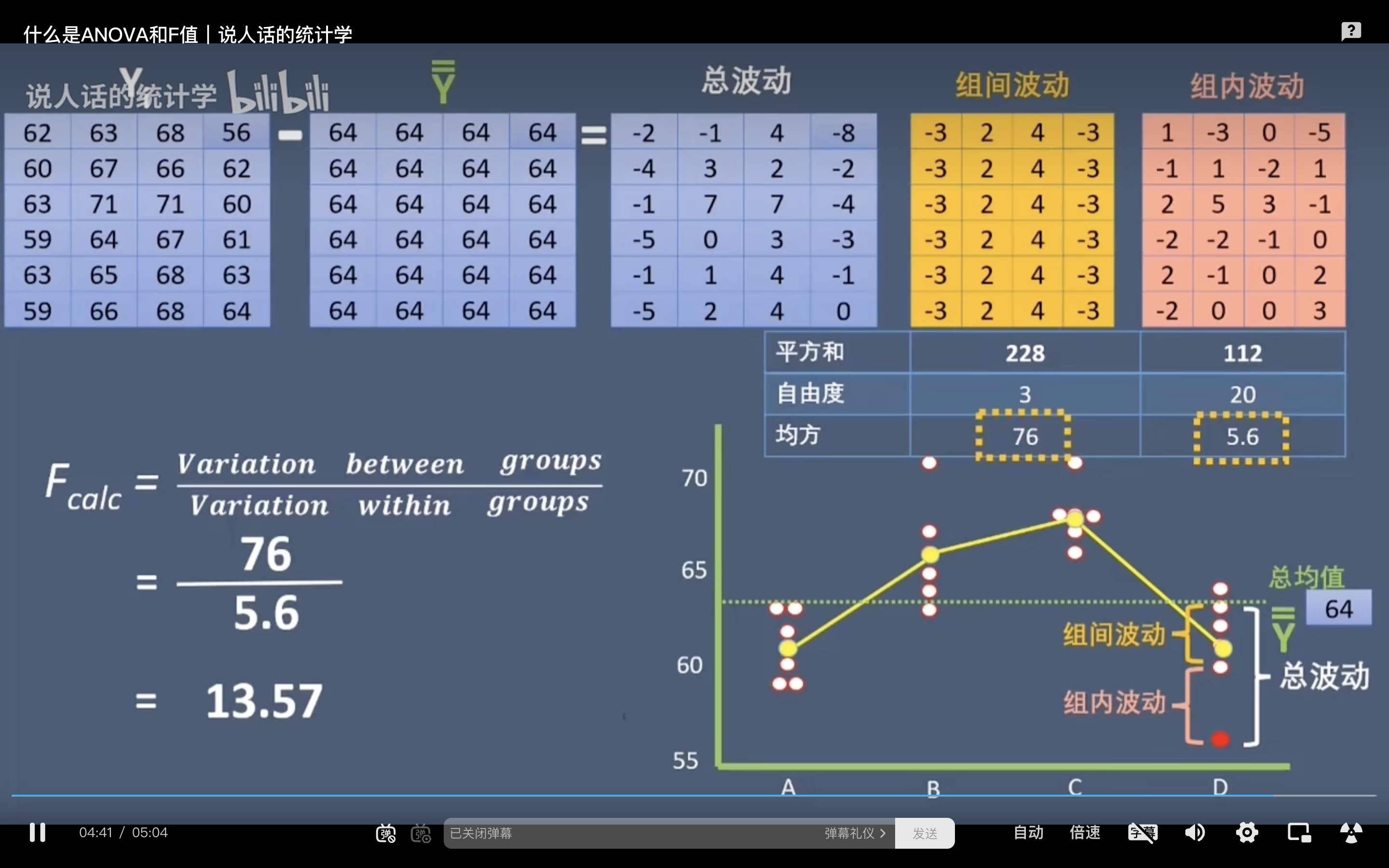
  • F值计算：

    • F-value = 组间波动 / 组内波动，如上图

  • 从上面的公式可以知道，F值越大，组间差异越大，各样本组之间存在差异的可能性越大。

  • 举个例子，下图中有四组小白鼠，每组六只，分别给了四种不同的麻醉药，想要证明至少有一种药和其他的不一样

    • H0：四种药的成分完全一致
    • H1：至少有一种药和其他的要不一样
    • 计算过程如图二
    • 计算出的F值为13.57，F-value = 组间波动 / 组内波动
    • 也就是说，F值越大，组间波动越大，越有可能说明至少有一种麻醉药成分和其他不一样。
    • 

9.3 相関の構造を探る

• 相関行列：p１６１の図

• 偏相関係数：x、y、z独立ではないので、二つの相関係数を計算したいと、三番目の変数の影響を取り除くないと、だめである、この場合に、使う。

• 因子分析（Factor Analysis）：データの中にある複雑な相関のパターンを見出すことができると、それに対応する理由を読み取って解釈することができる。

  • 少ない数の共通因子の和でうまく表現することを目指す ？？？？？？
  • 用于理解观察到的变量之间的潜在结构
  • 因子分析的基本假设是，观察到的变量是由一组共同的未观察到的因子所影响，而这些因子又与观察到的变量之间存在某种关系。
  • 因此，通过因子分析，我们试图识别出这些潜在的因子，并了解它们对观察到的变量的贡献程度。

  因子分析待研究（？？？？）

• pca：データを少ない変数で、表現したいときに使える

  • 「データが散らばっていない方向」というのは、どの観測値も似たような値を取っているということですから、その方向についてはデータを記述する変数を用意しなくても、情報が失われにくいわけである。

  • 第一主成分（横轴）就是方差最大的方向

  • 负荷量：指每个原始变量与主成分之间的相关性或贡献程度

    • 负荷量的绝对值：负荷量的绝对值表示了每个原始变量对主成分的重要性。绝对值越大，表示该原始变量对于主成分的贡献越大。
    • 正负号：负荷量的正负号表示了原始变量与主成分之间的方向关系。正号表示原始变量与主成分之间的正相关关系，负号表示负相关关系。
    • 解释方差比例：负荷量的平方可以解释原始变量的方差的比例。负荷量的平方和越大，表示主成分能够解释的原始变量的方差比例越高。

  • 主成分得点（Principal component score）:观察值变化坐标轴后的新坐标

• clustering：データの中の近い観測値同士をまとめてグループにすることで、データ全体をいくつかのまとまりとして把握することができる

  • 非階層的clustering（non-hierarchical clustering）：

    • Kmeans
    • GMM（Gaussian mixture model）
      • ？？？（待研究）

  • 階層的clustering (hierarchical clustering)

9.4 各種手法の整理

• 目的変数
• 説明変数

ch10 数理モデリングの要点

• 数理モデル：データからあるdiscipline存在するわけ、そのdisciplineは式で表す

• 数理モデルは三つの構成要素がある：

  • 変数
  • 数理構造
  • parameter

• データの質はモデルのparameterに影響をあげる、すなわち、モデルの質も影響をあげる

  • データが偏ると、モデルからの結論も偏る
  • その時点と場所のデータで作ったモデルは、その時点と場所の結論だけ出る。

• 適合度：拟合程度

• 決定係数：R square、说明拟合程度的参数，0-1，越大越好

10.2 目的に応じたモデリング

• 理解志向型モデリング（Understanding-orinted-modeling）：

  • 比如分析超市数据，分析什么样的顾客喜欢什么样的商品，从而制定销售策略（販売戦略）
  • 回帰モデル

• 応用志向型モデリング（Application-orinted-modeling）:

  • 予測やデータ生成など応用の性能を追求する。
  • 比如中国的交通管理系统，根据早晚高峰可以动态规划，减少等待时间
  • deep learning
    • for example：neural network

• モデルデータがよく記述できないとは、モデルを複雑させる必要がある

• 過学習：overfitting

• 汎化：generalization

10.3 モデルによる予測

• やすい：状況が確定すると、データ十分取られる

• にくい：

  • 状況が変わる
  • データが存在しない部分については全て考慮されない

• 内挿：データが周りに存在する領域において予測

• 外挿：データが存在しない領域において予測

• 線型：着目する要素同士が足し算・引き算（＋定数倍）の関係性で書けれる

• 非線型：〜書けれない

• 予測では、伝統的なAIモデルは、データ不足の場合、予測効果良くない、neural networkはデータが少ないでも、効果が良くなれる

ch11 データ分析の罠

11.1 データ操作に関する罠

• 割合を使うとき、情報が失うかもしれない、注意しなきゃ
• Simpon‘s Paradox：割合を見るとき、分層、グループ分けようなものを注意しなきゃ
• 平均値は極端的な値の影響を受けやすい
• 相関係数も極端的な値の影響を受けやすい
• 切り取り：特殊のデータは一般のデータとして扱わない注意しなきゃ
• グルフを歪めない：bar plotを描く時、棒の長さと値一致しなきゃ

11.2 手持ちのデータに関する罠

• 別の視点でデータを集められる
• データの質大切である

11.3 分析の目的に纏わる罠

• 結論のpattern：

  • 影響を与えていると考えられる
  • 影響を与えていると考えられない
  • このデータから何とも言えない

• 影響があることと、その結果が重要であるかは別の問題であるが、効果の強さを含めて総合的に結論を導くことも大切である

• 許容度：目的により、異なる、例えば：

  • 医学に応用する場合に、許容度が小さく設置する
  • 天気予測の場合、大きいでもいける

• モデルに信用すぎるダメ

• 目的に応じた分析のデザイン：

  • データが多くなると、一般的な場合で、モデルの精度も上がるが、データを集めるため、モデルをtrainためのコストも上がる
  • 適度のモデルをデザインするのは大切である
  • また、for trainging model,what data do we need is always important.

ch12 データ解釈の罠

12.1 分析結果の信頼性

• 再現性（Reproducibility）があるかどうか、考慮しなきゃ
• 再現性：取られた結論は、たまたまですか
• HARKing:データ分析してから、仮設を作る。ほぼ再現できない
• P-hacking:p-valueは有意水準より大きい場合に、いろいろな方法で処理し、pーvalueは有意水準のいかにさせる。学術不正行為である。
• Hillの基準：因果関係を判定するため。

12.2 解釈時に生じる認知バイアス

• 避けるために：

  • １次元の情報に基づいて結論を導くのではなく、多元的な情報を集めて、総合的な結論を出す
  • 弱い結果からある解釈が見えた場合、追加でそれを示す実験を行ったり、独立したデータを取得して分析するなどして、信頼性がある結果を得て初めて強い主張ができる
  • 「証拠を見る限り、どう考えてもそのように解釈するのが妥当である」という結果が得られて、初めて強い主張ができると考えるのがいいである。

• 因果の誤謬：ある事象Aが起きた後に別の事象Bが起きた時、「AがBの原因となった」と考えてしまう

• gambler’s fallacy（ギャンブラーの誤謬）：ある事象がたまたま連続して起こった後には、発生確率が小さくなると考えてしまう

  • 例えば、コイントス５回は正になると、次は反だと思う。
  • コイントスの事件がそれそれ独立である

• 利用可能性バイアス：ある可能性に過度に焦点を当て、他の可能性を無視することで、合理性を欠いた決定を引き起こす。

  • 発生確率が低い事象についてはデータが存在しないことが多く、理論による外挿が必要になることもしばしばである

  • データ活用の場面では、このような状況に対応する必要があるかも含め、どのようなケースではうまく動き、どのようなケースではうまく動かないのかという、数理モデルの適用範囲を事前に考えておくのが良いである。

  • 利用可能バイアスは、データ分析において分析者の事前予想に影響を与える。

• 確証バイアス：自分の仮説を検証する際には、それを支持する情報ばかり集める、逆に反証となるような情報を無視したり集めようとしない傾向のことである。

ch13データ活用の罠

13.1 目的に基づいた評価・意思決定

• 流れとして：
  • Page259の図13.１.１である

13.2 データの取得と活用

• 処理コストを下げるために：

  • 固定的な形を挙げて
  • 数値コードを用いて曖昧がない回答を集める

• データ取得の計画

  • 初心者は、交絡因子などを軽視して、「とりあえずデータさえとれば、後は何とかなるだろう」という考えでデータを集めてしまうことである。

  • 避けるために、事前にしっかり対象を調査し（場合によっては小さいデータセットで分析作業を行い）、どのようにしてデータを取れば良いかということも含めて設計することが大切である。

  • データを取る負担を考える：

    • 何の目的で、どのような方法で分析し、結果から何を結論付けるか（データ活用の文脈では、さらにどう行動するか）を事前に決め、得られる利益が、それを行うために必要な金銭的・時間的またはその他のコストに見合うかを検討するステップが大切である。

13.3 現実世界とデータ分析

• データによる管理主義

  • 「測定できないものは管理できない」
  • この考え方は、一定の成果を収めてきましたが、簡単に測定できる指標に偏重した物の見方を助長したと言ってもいいでしょう。このような状況では、数値化しにくい指標はしばしば置き去りにされ、本質的に重要なことが見逃しされやすくなる。

• Hackされる評価指標

  • 「測れないものは改善できない」おいう思想がある。

  • 測りにくいもの、測れないものに対しても同じような管理を行うとすると、種々の問題が発生する。

  • 「ある指標を目標指標に設定した瞬間に、その指標は指標としての価値を失う」ことはさまざまな分野で指摘されている。

    • 例えば、医師の手術のスキルを評価するのに、「手術の成功率」のような指標を使ってしまうと、難しい手術を引き受けないというインセンティブが動く

  • このような、簡単に数値で測れないものを無理やり数値指標に落とし込んでしまうと、その指標で考慮されていない抜け穴を使ってハックされてしまう。

  • データから様々な有力な指標を作ることができたとしても、それを「実装」する際には、安易にその指標に頼りきりになるのではなく（補佐的に利用するのは問題ないでしょう）、それによって測られる人々がどう反応するかまで慎重に検討する必要がある。

言葉

Japanese	English・Chinese
収まる（おさまる）	store
狭る（せまる）	narrow
便宜（ベンぎ）	cheap
部分集合	Subset
デュ	dlyu
〜がち	often
逐一（ちくいち）	One by one
検める（あらためる）	check
媒体（ばいたい）	Media
脆弱（ぜいじゃく）	weak
譲渡（じょうと）	Transfer （this right to you）
	Scm is short for Supply Chain Management
罠（わな）	min（二声）
裾（すそ）	tail
度合い	how + adj
プロット	plot
足掛かる	Be going to start
見つけ出す	find out
探る	explore
散らばる（ちらばる）	dispersed（The data's dispersed/scattered）
まとまり	grouping
振る舞い	behavior
	Oriented　导向
置き去る（おきさる）	ignore
頼りきる	Rely on sth too much